Introduction
The Arithmophone project started out of a desire to explore some alternatives to 12 tone equal temperament (12tET), the tuning system that so completely dominates Western music that many people don’t even realise that other options exist. This is not without its reasons: there are many advantages to 12tET and as soon as you start trying to design an instrument based on other principles, you run in to all kinds of complexities. Over the course of about 18 months, I made many different designs and developed them to various degrees of functionality. In the end, I decided to focus my attention on 3 separate ‘instruments’, each with its own design goals and priorities. These instruments are:
- The ToneHive. This is the first design that came to fruition. Its main design goal was to provide a good selection of just intonation intervals in a form that is relatively straightforward to play. The selection of notes has at its main priorities: to provide a good amount of harmonic flexibility and to ’emancipate’ the 7th harmonic to bring it on equal footing with the 3rd and 5th harmonics.
- The EDO. This design was made with the goal of exploring and comparing different equal temperament systems. Specifically, it offers 31 tone equal temperament alongside 12tET in order to highlight the strengths and limitations of each system.
- The Korale. The goal of this design was to make a just intonation instrument that is as accessible and easy to play as possible, even on small devices. It is by far the most complicated of these three instruments, but it hides a lot of this complexity behind a menu of preset pentatonic and diatonic scales.
In this article, I will start by describing some general design principles behind the Arithmophonic designs: two dimensional layouts, colour coded keys, octave grouping and symmetry. I will then go on to describe each of the three instruments in more detail.
Please note: the following sections assume a basic understanding of musical notes and intervals, just intonation ratios and temperaments. If you are unfamiliar with these things, everything you need to know can be found in this article.
Two-dimensional keyboards
On a standard piano keyboard, the notes are arranged from low to high (going from left to right). Although the keyboard itself is a 3-dimensional thing, with its raised black keys, this layout is basically one-dimensional: all the notes are arranged along a single line.
The Arithmophone designs on the other hand, use a two-dimensional grid. Arranging the notes in two dimensions instead of one has some interesting advantages, especially for an on-screen keyboard: it can help to make the relationship between different notes more intuitive, make many chords and melodies easier to play and it also makes more efficient use of the available space on the screen.
When we arrange the notes in two dimensions, it no longer makes sense to order them simply from lowest to highest, so we need to find some other way of arranging them. We can start by selecting some ratio, for example 3/1, and placing the same ratio between each pair of adjacent notes, like this:
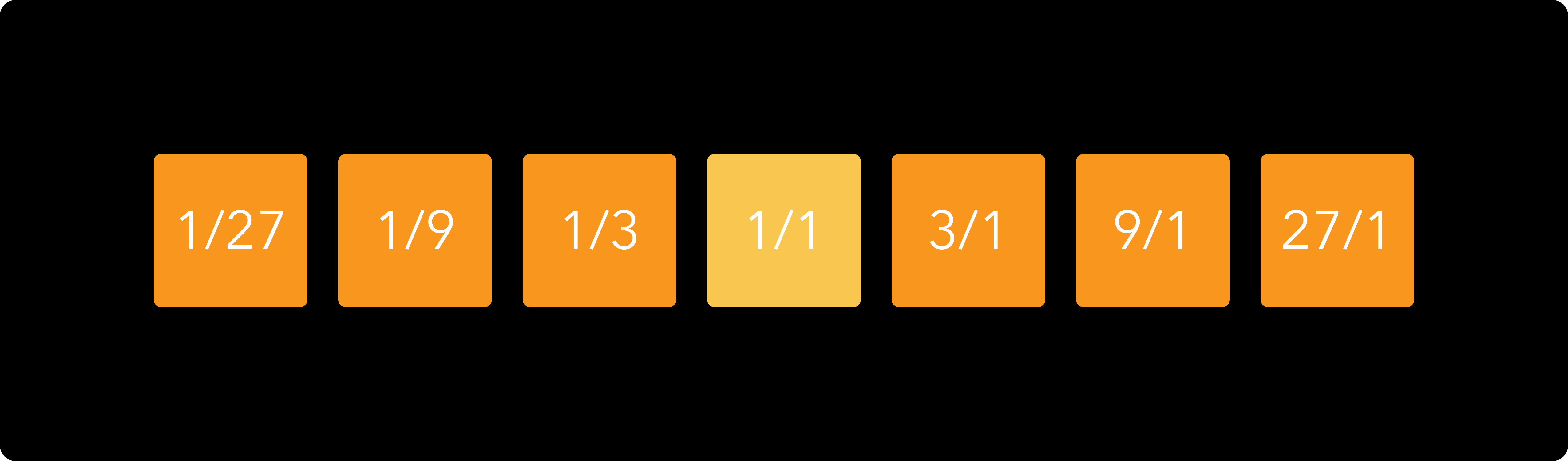
These numbers represent the ratios of the frequencies: if the 1/1 note has a frequency of 100 Hertz, then the 3/1 note is 300 Hertz (3*100), et cetera. Each note has a frequency that is three times as high as the note to the left of it. In terms of standard note names, taking D as the central note, this example looks as follows:

Once we have this first row of notes, we can chose a different ratio, for example 5/1, for the notes above and below, like such:

With note names instead of ratios it now looks like this:
By filling out the other columns we can make a grid like this:
This is how many musically useful intervals arise. The ratio 3/5 does not appear as a direct over- or undertone of the 1/1 note, but it is present in the column of the 3/1 note and in this way it is strongly (though indirectly) related to the 1/1 as well. 3/5 is in fact the note known as the just minor third, a very common note in almost any kind of music.
With note names instead of ratios, our square looks like this:

This type of keyboard layout is called isomorphic. That means that wherever you are on the keyboard, moving a certain step always results in the same musical interval. In this example, if you move one step up, you always get a major third, et cetera. Unlike on a piano, once you have learned a certain pattern, chord or melody in one key, you can play it in any other key just as easily.
In standard tuning, this pattern starts repeating pretty quickly, because many keys with different note names are actually the same note. On a piano, G# and Ab for example, are really just different names for the same key. In just intonation, this is not the case, and each key has its own note. G# is a different note from Ab, and even the two Bb’s in the grid above, although they have exactly the same name, are actually different notes.
This kind of isomorphic grid works very well for tempered tunings, and in the Arithmophone, variations of this layout are used for the ‘EDO’ keyboard styles (12 tone and 31 tone equal temperament). It does not work so well for a just intonation keyboard, because there it generates infinitely many different notes, many of which are not very relevant musically speaking. So for the ‘ToneHive’ just intonation, a different approach was needed.
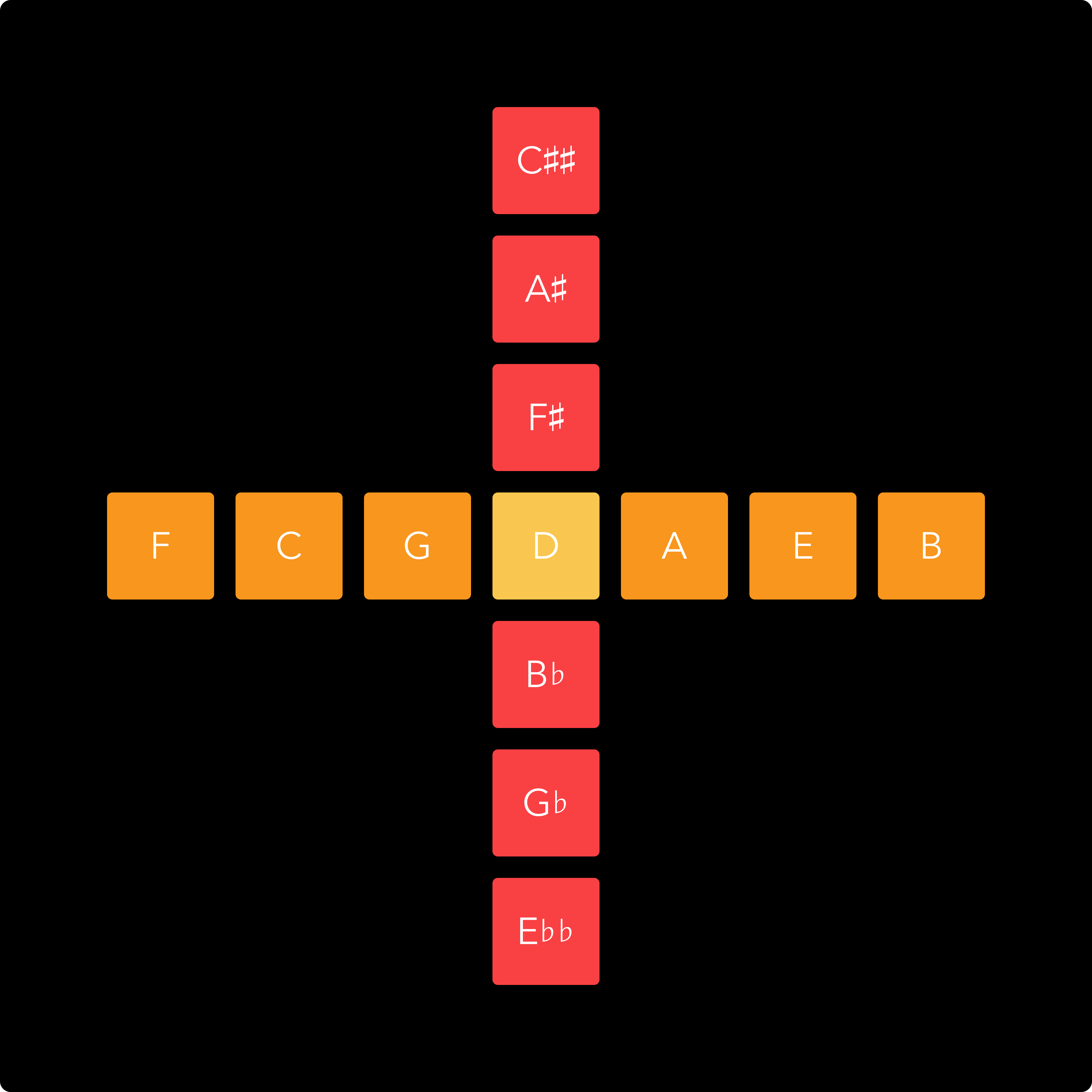
This keyboards is based on what I call ‘harmonic spines’. A harmonic spine is a set of notes that are directly under- and overtonal to a central note. A basic harmonic spine looks like this:
This spine contains all overtones and undertones of the central 1/1 note up to the seventh harmonic. It could be extended further in both directions, to include the ninth harmonic, the eleventh harmonic et cetera.
Only odd numbers are included, because even numbers don’t introduce any new notes. Those are simply octaves above and below existing notes: 6/1 is an octave above 3/1 and so on. The 1/1 note forms the center of the keyboard, but a harmonic spine does not have to start on this note, it can be constructed from any note. The example below shows a secondary harmonic spine starting on the 3/1 note.
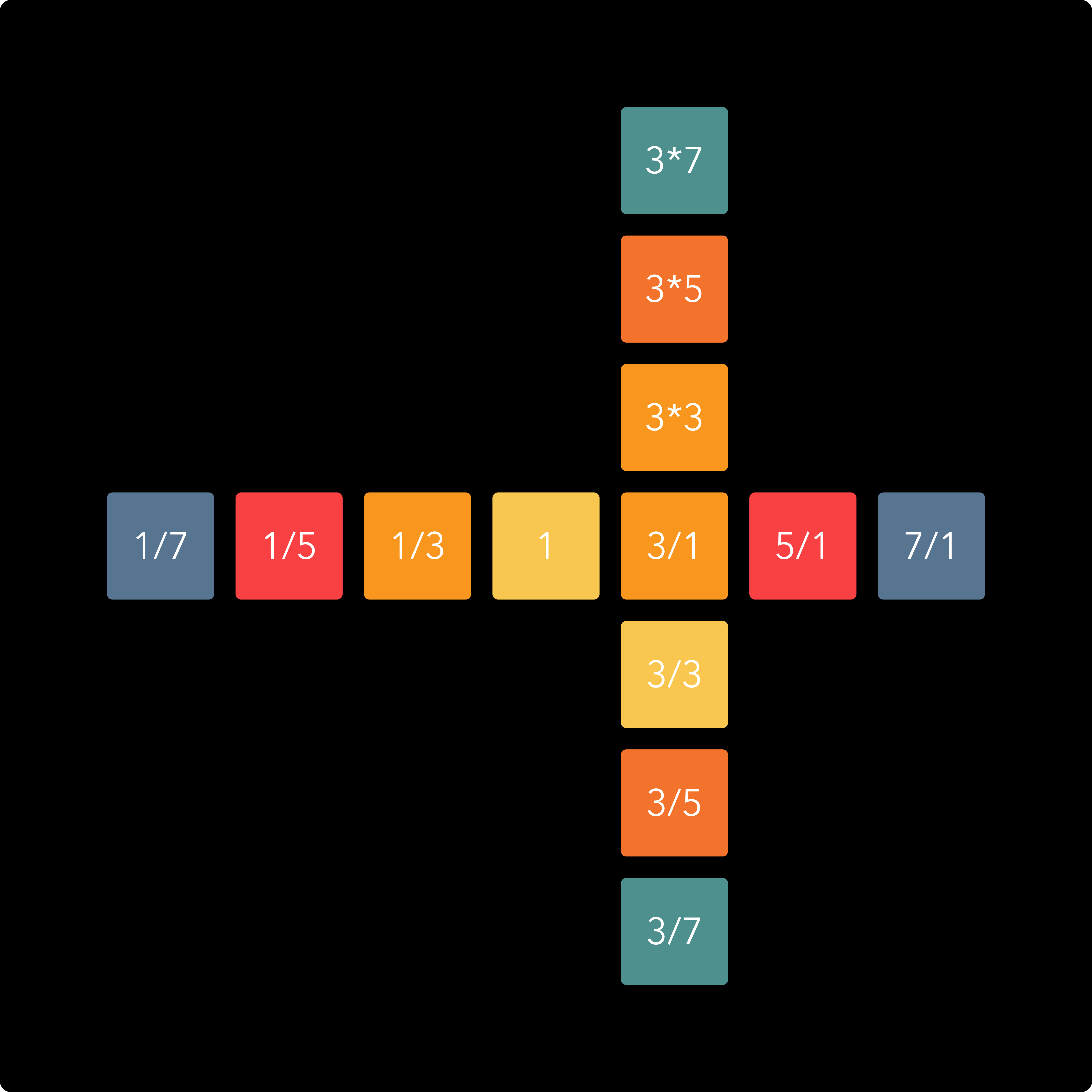
When we extend this principle and use it to make a square of harmonic spines, we obtain many of the most common musical intervals:

However, as a musical keyboard this layout is not very efficient. It generates a lot of duplicates: the same ratios appearing in different places. To remedy this problem, we start by folding the central harmonic spine around the 1/1 ratio like this:

If we start filling in the secondary harmonic spines now, we will see that most of the duplicates land in the same place and therefore become a single key. First we fill in the spines in the inward direction:
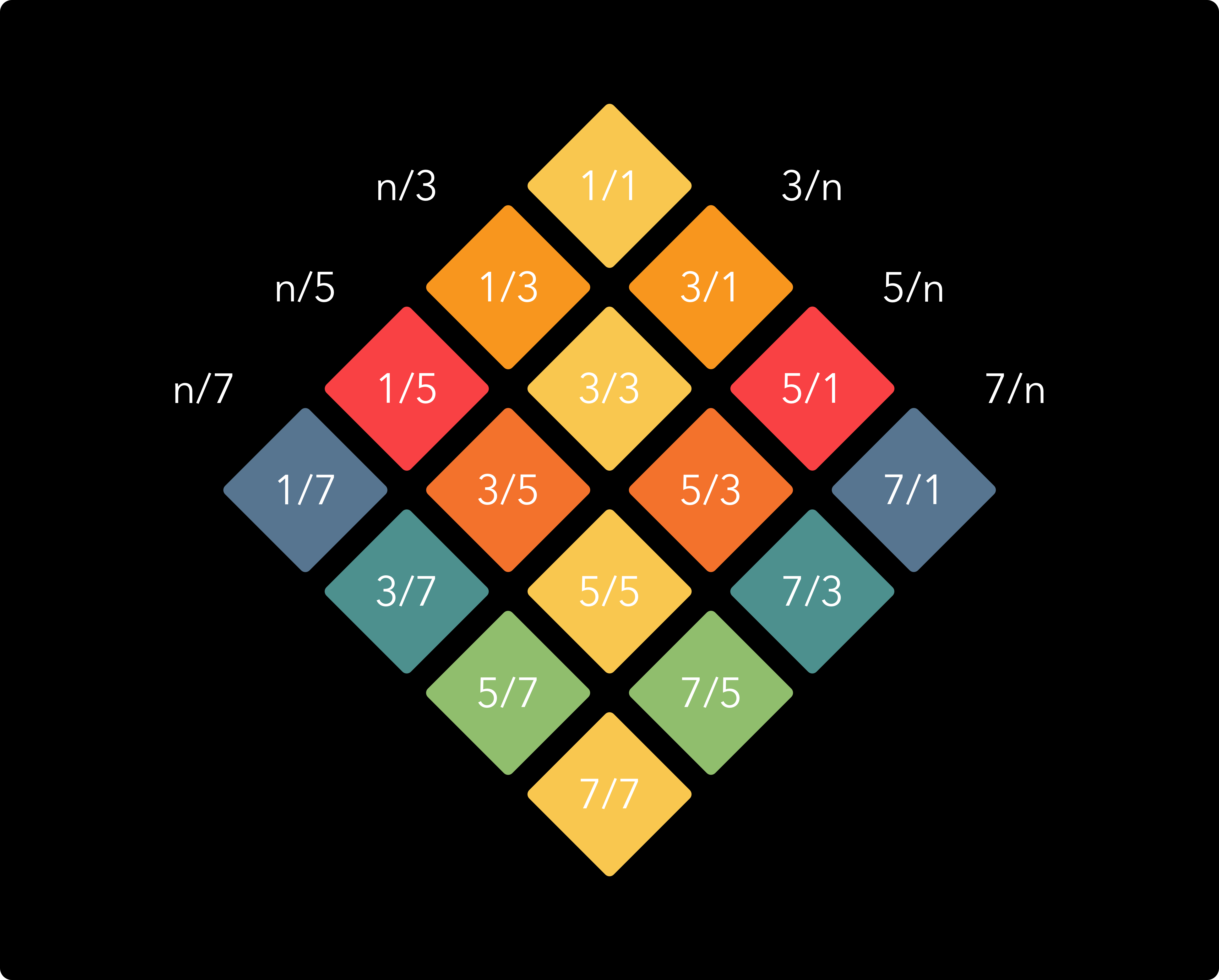
And then we complete it in the outward direction:

Now we have all the same intervals as in the square layout, but we only need slightly more than half the keys. This intertwining of harmonic spines forms the basic harmonic structure of the ToneHive keyboard style.
Colour coded keys
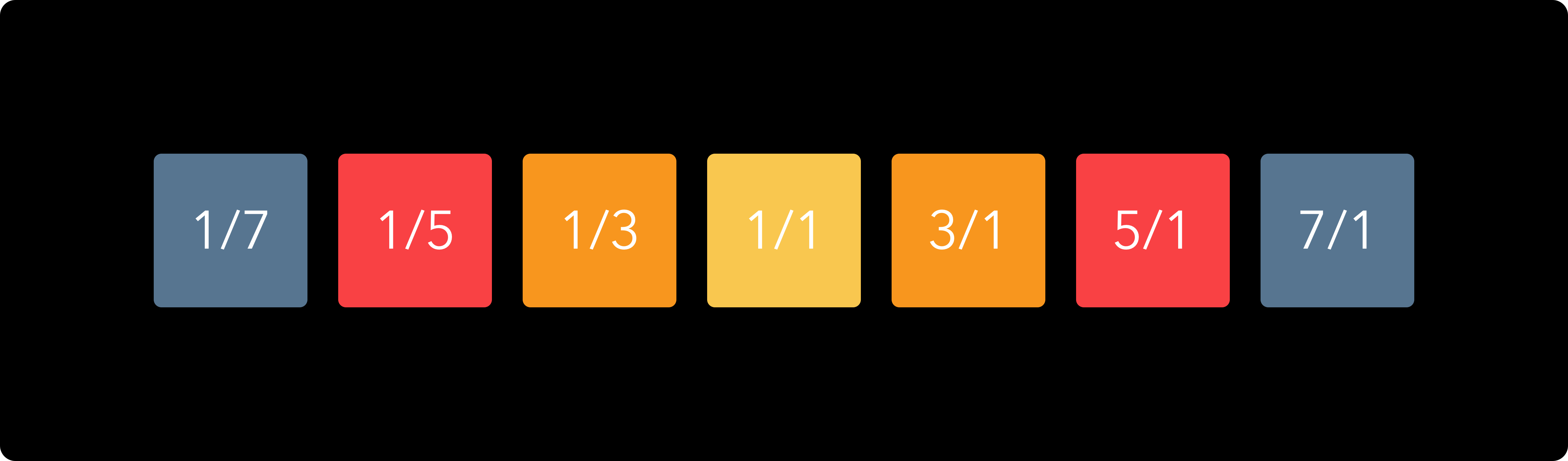
On the Arithmophone, the colours of the keys reflect the nature of the interval they form with the central note. This provides a visual aid for navigating the keyboards. On the ToneHive, the colouring works as follows:

The Arithmophone EDO keyboards use equal temperament tuning, so their keys do not correspond directly to any ratio. However, they do approximate certain ratios (this is the very reason that equal temperaments work in a musical sense). The keys on the EDO keyboards are coloured according to the following scheme:

Since the ratios selected and the corresponding colour scheme are approximate, they are just one possible interpretation among many. For example, the key with ratio 13/1 inscribed produces a note whose frequency is actually more closely approximated by the ratio 105/1. In cases like these, I have chosen the simplest ratio that provides a fairly close approximation (with ‘simple’ interpreted as ‘consisting of small numbers’).
Finally, on the Arithmophone Korale, I have taken a different approach to colouring the keys. Because the Korale only uses diatonic and pentatonic scales, it never offers more than 7 different notes at a time. These notes are coloured according to their scale position, like this:

Another way of looking at it, which might make the colouring easier to understand, is like this:

For each of these colour schemes, there is some meaningful connection between the colours of the keys and the “sound colours” of the notes they produce, in relation to the central note. These connections are not always straightforward, but I hope they will reveal themselves by playing around with the Arithmophone, and provide some insight and inspiration along the way.
Octave grouping
Unlike on most instruments, the distance between notes on the Arithmophone does not correspond to their distance in pitch, but to their harmonic distance. Because the shortest possible harmonic distance is the octave, it seemed logical to group together different octaves of the same notes. This also solves a problem inherent in using scales with more than 12 notes per octave, namely that they can become very unwieldy. Using octave grouping allows for a clean and relatively simple keyboard design that still spans a range of several octaves. On the ToneHive, 3 octaves of each note are grouped together. On the EDO, octaves come in groups of 2, though this can also be switched to 3 in the MIDI version.
Symmetry
The symmetry between harmonic intervals is a very important aspect of music, yet is not usually represented in the design of musical instruments. The design of the Arithmophone ToneHive is fully symmetrical. Intervals that are mainly overtonal (formed by multiplication) are on the right hand side of the keyboard, and intervals that are mainly undertonal (formed by division) on the left hand side. On the Arithmophone EDO, the same symmetry is represented, though here it is slightly skewed. This is a natural consequence of equal temperament, which skews harmonic ratios in order to make them fit a repeating pattern.
The ToneHive
The ToneHive keyboard uses just intonation tuning in a 7-limit system. Because 7 is the limiting prime factor allowed in this system, the ToneHive does not feature any ratios containing primes above 7. All ratios with numbers larger than 7 are combinations of smaller factors, for example 9/8 can be rewritten as (3*3)/(2*2*2).
In standard tuning (12 tone equal temperament) only ratios up to prime limit 5 are represented. Expanding this limit to 7 introduces a whole new class of notes, that are not really represented Western music theory, although they do appear frequently in Blues and Jazz, at least on instruments with flexible tuning like slide guitars and saxophones (and of course in singing). These notes are often referred to as ‘blue notes’, a fact I have used as inspiration for the colour scheme of this keyboard.
Some notes with 7-ratios are extremely close in pitch to notes with 5-limit ratios, for example 7/5 and 45/1. After octave reduction, the interval between these notes is only 225/224, very close to 1/1 (if the interval were exactly one, that would mean they were the same note). These notes are almost interchangeable. For example, if we start on 9/1 and want to add a major third above, we would normally use 45/1 (because 9*5 is 45). But if we use 7/5 instead, we still hear a very convincing major third. In fact, it is much more accurate than the major third we are used to in standard tuning: whereas the major third on a well tempered piano deviates from the pure 5 ratio by about 14 cents, this switch between 45/1 and 7/5 results in a deviation of only 7 cents (a cent is 1/1200 of an octave, or 1% of a standard semitone).
The ToneHive layout is based on harmonic spines. However, in order to create an interesting and coherent selection of notes, I have taken quite a few liberties with the basic structure in this case. The harmonic spine is only followed up to the 7th harmonic, multiples like 9 and 25 don’t get their own spine anymore. Instead, I have created a ring of notes around each of the intervals 7/1 and 1/7, coloured in shades of blue and green, filled out with a few remaining 5-limit notes that don’t appear in the basic spines but are still relevant in this musical context.
In basic ratios, the final result is as follows:
This makes for three different areas: the notes in yellow, orange and red are all centered around the 1/1. The blue and green notes on the left are centered around 1/7 and form their own coherent set of chords and scales. The same thing applies to the blue and green notes on the right, except that those are centered around 7/1. These areas are connected in two different ways: by a direct leap of 7/1 or 1/7, but also by the close connections created by the 225/224 exchange.
Because the illustration above contains a lot of numbers, it may not be very easy to digest. Below I have included an illustration with note names instead of ratios, using the note “D” for the 1/1 ratio. This is a lot easier to read, however, in 7-limit just intonation the mapping of ratios to note names is quite tricky. For example, the note “C” now stands for 3 different ratios: 9/5, 16/9 and 7/4. These are really 3 different notes that are around the same pitch but have very different harmonic functions.
It should be remembered that note names and scale degrees are only labels, ones that work very well for 5-limit just intonation and for 12 tone equal temperament, but not necessarily for other tuning systems. I’ve found that in the 7-limit system, it is best to get to know each note for what it is of itself, and forget about the standard nomenclature as much as possible.

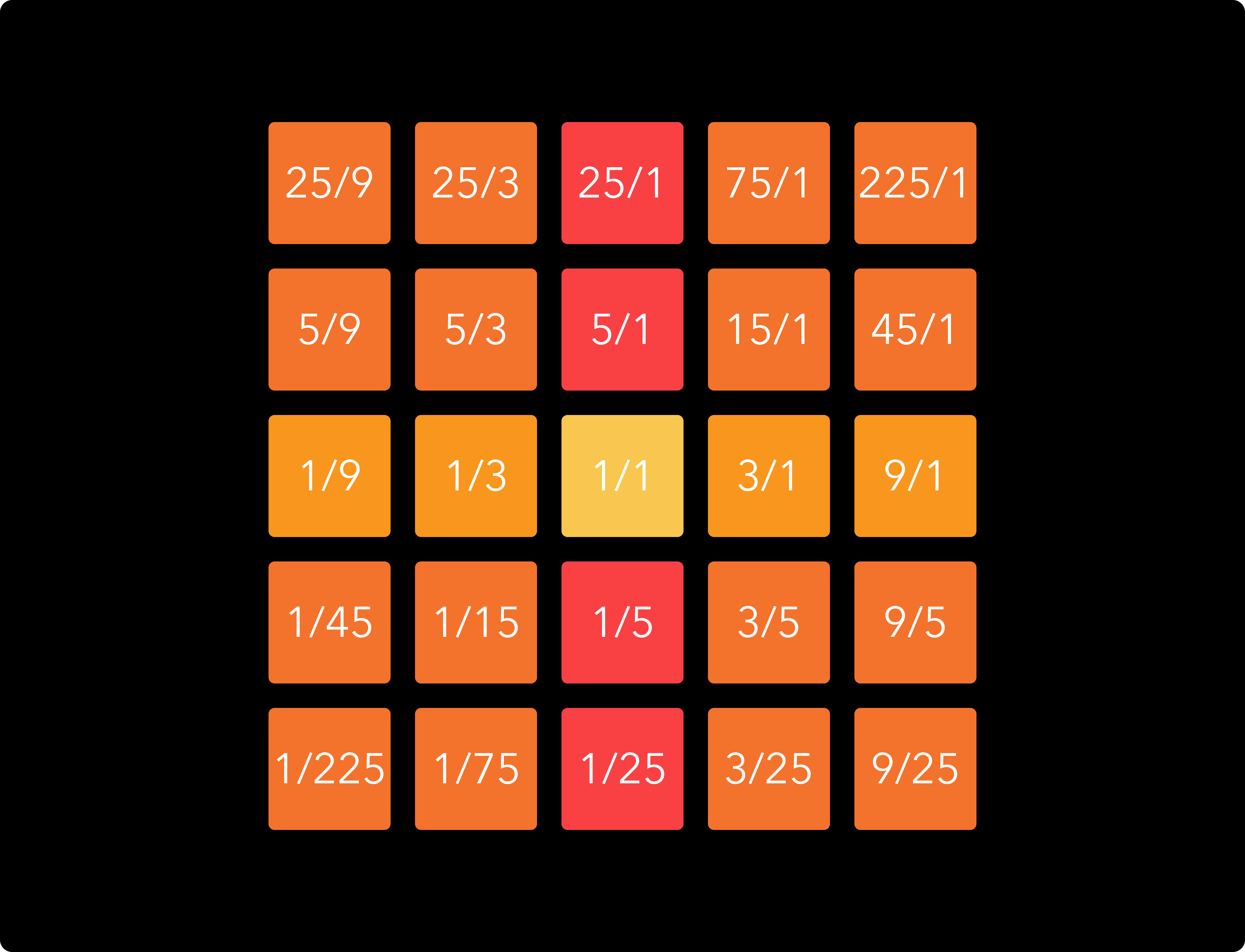
There is another way of representing the notes on the ToneHive that I have found helpful, and that is in a “quasi 3-5 grid”, where 7/1 takes the place of 225/1 et cetera to form an extended 5-limit system, like so:

This shows how the 7-limit notes can double as extensions of the central 5-limit notes (and vice versa). Of course, from this perspective they are no longer perfectly tuned, but the discrepancy is small enough that they can be convincingly used. For example: a fifth above 25/1 would be 75/1, this note is not present on the ToneHive. But the jump from 25/16 to 7/3 is only 7.7 cents off from a perfect fifth. And there are other ‘harmonic wormholes’ to be found in the ToneHive keyboard. For example, the jump from 35/1 to 3/35 (or 35/32 to 48/35, after octave reduction) is only 5.4 cents removed from a just major third. Considering the fact that we routinely accept the 13.7 cents tuning error that 12 tone equal temperament causes for the major third, these tuning errors are quite modest. This means that with some careful planning, we can modulate ‘all the way around’ on the ToneHive, giving it considerable harmonic flexibility. In the next illustration, I have connected four copies of the ToneHive “quasi 3-5 grid” together to further illustrate these harmonic connections.

The ‘hole’ in the middle of this diagram makes clear that the note selection of the ToneHive could also be seen as part of a larger temperament. We could complete this by adding 12 more ratios, shown below in grey:

This creates a 53 note ‘well temperament’ with some very interesting properties. It contains many just intonation intervals, yet it also functions as a complete 5-limit temperament with tuning errors that never exceed 7.7 cents. Although this is a bit beyond the possibilities actually present on the ToneHive, I believe this could be a very interesting compositional system. Of course it does require 53 notes per octave, at which point one could also consider using 53tET. In fact, the ToneHive keyboard could also work quite well tuned to 41-out-of-53 equal temperament, like so:

In 53tET, both thirds and fifths are nearly perfect, so from the 5-limit perpective, this would certainly be preferable. However, the 7th harmonic in 53tET is off by about 4.8 cents, so from a 7-limit perspective the 53 note “well temperament” presented above might actually be more advantageous.
The EDO
31 tone equal temperament (31tET) is a very interesting alternative to the much more common 12 tone variety. It has a history that goes back to the sixteenth century, long before 12 tone equal temperament became the standard in Western music. It offers a superior approximation of rational intervals while still maintaining all the flexibility of an equal tempered system. Having more different notes, it is also more complicated, both for the mechanical construction of instruments and in the ease of playing them. In the end, the simpler 12 tone system proved ‘close enough’ for Western music and 12tET became the dominant system from the 18th century onwards. This makes a lot of sense considering the fact that the music of that time period was mainly based on a 5-limit harmonic system. However once you start requiring the inclusion of higher harmonics, the balance quickly shifts toward 31tET.
When you divide the octave in to twelve equal steps, you get a very good approximation of the 3rd harmonic and a more or less passable approximation of the 5th harmonic. When you divide it in to 31 equal steps, you get an almost perfect approximation of the 5th harmonic while the 3rd harmonic is only slightly less accurate. You also get an excellent representation of the 7th harmonic and pretty decent approximations of the 11th and 13th harmonic. In the 12 tone system, these last three are lost entirely.
Using the 31 tone system provides many rewards, but finding your way around 31 equally spaced notes without a clear tonal center is not necessarily an easy thing. So it was an interesting challenge to try and make a keyboard that presents these notes in a reasonably intuitive way. I started out by making a 4 by 8 grid, containing just enough keys for a full octave, and arranging the notes so that each step up is always a fifth and each step to the right a major third. This is achieved by jumping 10 notes for every third and 18 notes for the fifths (just as you would jump 4 notes for every third and 7 notes for every fifth in the 12 tone system). Numbering the notes from lowest to highest, the arrangement looks like this:

I then coloured the notes based on the ratios they most closely approximate (see the paragraph ‘colour coded keys’ above), taking the first note as root. It then looks like this:
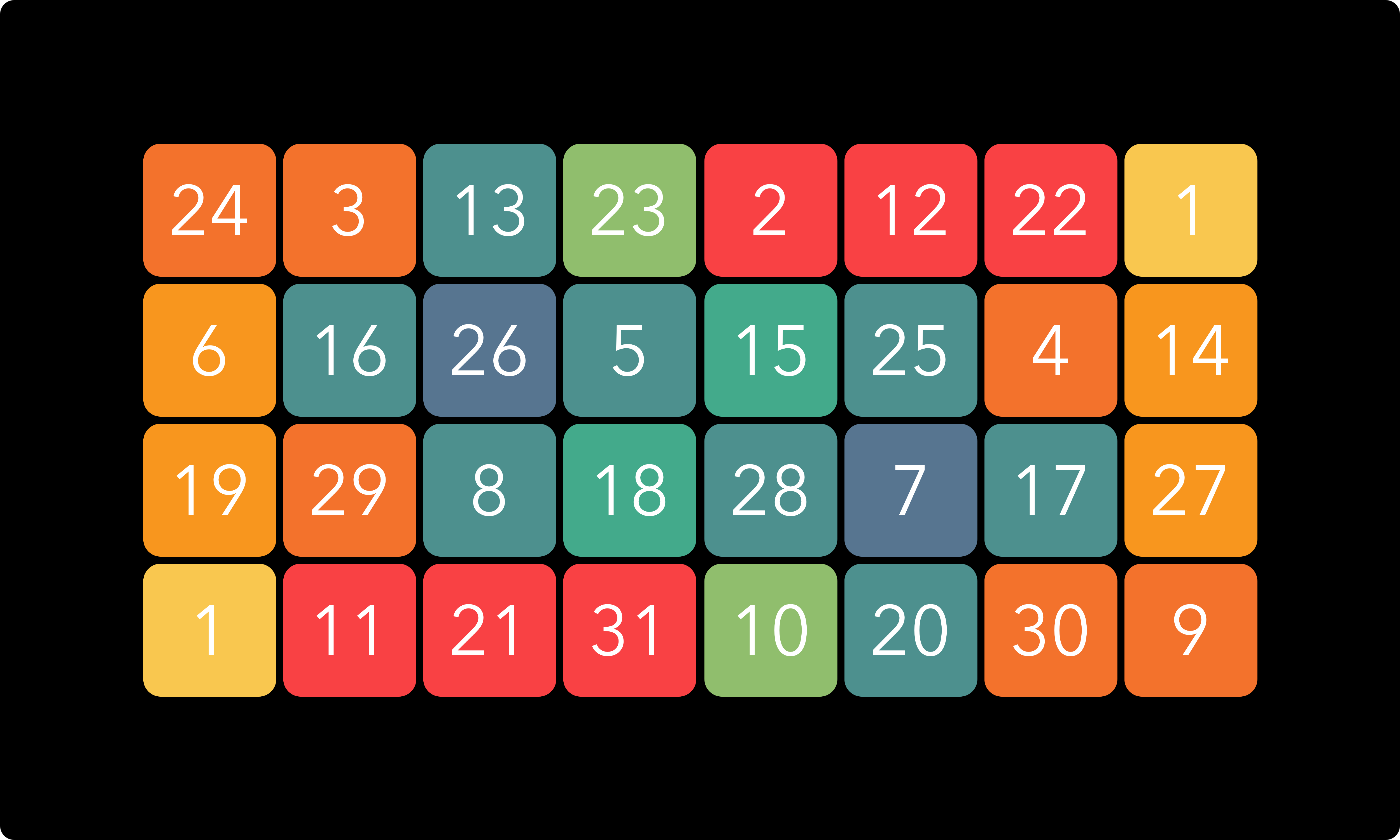
The more familiar ratios (those that are also present in 5-limit just intonation and 12 tone equal temperament) are mainly on the left and right sides of the grid, with the more exotic intervals mainly in the middle. I thought it would be better to have the most common ratios grouped together in the center, so by splitting the grid down the middle and then moving the halves around and lining them up to maintain the harmonic pattern, I obtained this arrangement:

This layout has some interesting properties. First, the broken-up shape, along with the colouring, provides some useful visual clues for navigating the keyboard. Second, the central columns now provide clear and easy access to all the most common diatonic scales. The middle two columns produce the Dorian mode, the most symmetrical and arguably the most universal of all the diatonic scales. Other modes like Ionian (major) and Aeolian (natural minor) are found by substituting one or two notes from the columns directly to the left and right. These scales sound slightly different in 31 tone equal temperament than in 12 tone equal temperament, closer to just intonation and with a wonderfully stable and earthy quality to them.
Below are the ratios that best approximate the notes of 31 tone equal temperament to my ears. You can see that the whole tone, or major second, is ambiguous in this case, falling right in between the 9/1 and 5/9 ratios (the same goes for the minor seventh which is a whole tone down rather than up, falling between 1/9 and 9/5). This kind of tuning is also known as a meantone tuning, and that is where the name comes from: the tempered whole tone takes the mean of the two different just intonation whole tones.
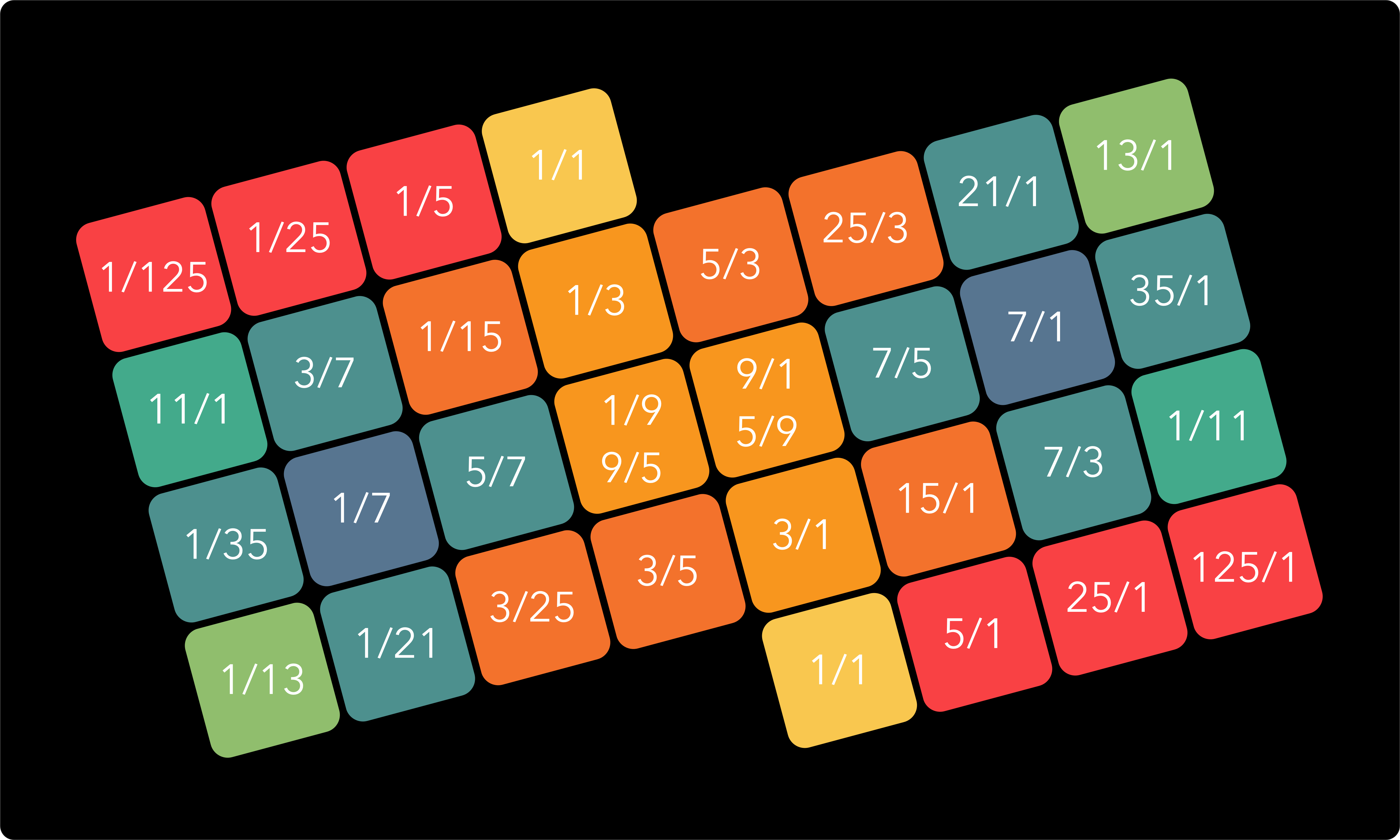
For easier reference, below is another illustration showing note names. This follows the double sharp/double flat convention for 31tET. There is a different convention also used for naming the note in 31tET, using half flats and half sharps. To my understanding, both of these are equally valid, however I have chosen to use the ‘double’ version for two reasons: first, half sharps and half flats are a typographical nightmare because the corresponding symbols are very poorly supported, not being part of any standard font or character sets. Second, the ‘double’ version provides a nice correspondence between sharps and overtones on the one (right hand) side and flats and undertones on the other (left hand) side. Interestingly, this does cause a bit of a discrepancy with the naming convention I chose for the ToneHive just intonation keyboard. Whereas the 7th harmonic is represented there by the note name “C”, on the EDO this becomes “B#”. There is something to be said for both ways. Using “C” creates a simple correspondence between ‘7th harmonic’ and ‘7th note of the scale’ which can help reduce confusion. Also, in blues and jazz, the 7th harmonic is generally interpreted as a (very) flat seventh. However, using “B#” helps to strengthen the distinction between the 5-limit “C” on the one side and the 7th harmonic, which really is something else, on the other side.

At some point, I realised that the keyboard arrangement I made for 31tET could also be interesting for ‘good old’ 12tET, which clearly shows it limitations in a direct comparison with 31tET, but also its advantages: because of the lower number of different notes, it becomes possible to extend the range of the keyboard and it also becomes a lot easier to play the same notes (in different registers) with the left and right hands, as one would on a piano. The 12-EDO keyboard is constructed like this:

Some notes are repeated twice across the keyboard, some only once. In terms of ratios, it works out like this:

And in terms of note names, like this:

In this case, Bb is identical to A# et cetera. To keep the illustration clean, I haven’t shown all the enharmonic spellings, only the most logical ones from the perspective of the key of D.
The Korale
The layout of the keys on the Arithmophone Korale was inspired by the Kora, a West-African harp. The Kora has 21 strings, 11 on the left hand side and 10 on the right. The strings are tuned to a diatonic scale (a scale with 7 different notes).

In diatonic mode, the Arithmophone Korale closely follows the note pattern of the Kora, with 11 notes on the left side and 10 on the right. The notes are arranged in such a way that scales (and scale-like melodies) are easily played by alternating the left and right hand. The notes cover a range of two complete octaves in the middle, with incomplete octaves above and below.

In pentatonic mode, the Arithmophone Korale provides scales with only 5 different notes per octave (the name comes from ‘penta’, the Greek word for ‘five’). Pentatonic scales are also very common in many kinds of music, from traditional bamboo flute to heavy metal guitar.
On the Arithmophone Korale, the pentatonic keyboard features 17 keys (9 on the left, 8 on the right). Because there are fewer notes, we also need less keys to obtain the same range. In fact, the pentatonic keyboard goes slightly higher than the diatonic one. This also means that the keys are slightly larger, making them easier to play on smaller screens. An added benefit of pentatonic scales is that there are very few “wrong” sounding note combinations, making them very beginner-friendly.

All scales on the Korale offer a 5 or 7 note selection from an underlying 21-note scale. The complete scale is presented in the diagram below. Please note: the middle three rows follow the pattern of a 3-5 grid, the notes in the top and bottom rows are 7-limit ratios added on to this.

This allows for a number of alternatives for each scale position scale position:
1st note of the scale: 1/1
2nd note of the scale: 1/15 (minor second), 5/9, 9/1 (major seconds) or 1/7 (septimal major second)
3rd note of the scale: 7/3 (septimal minor third), 1/27, 3/5 (minor third) or 5/1 (major third)
4th note of the scale: 1/3 (perfect fourth) or 45/1 (augmented fourth)
5th note of the scale: 1/45 (diminished fifth) or 3/1 (perfect fifth)
6th note of the scale: 1/5 (minor sixth), 5/3, 27/1 (major sixth) or 3/7 (septimal major sixth)
7th note of the scale: 7/1 (septimal minor seventh), 1/9, 9/5 (minor seventh) or 15/1 (major seventh).
In just intonation, there is usually more than one way to create a specific scale. In 12 tone equal temperament, there is just one set of notes that produces a D Dorian scale, but in just intonation there are many. I have distinguished some of the possibilities and and labeled them as different types in the illustration below.

The “Type A” and “Type B” scales shown in this illustration are both major (Ionian) scales and in equal temperament they would be identical. With the note D taken as 1/1, they both produce the notes D, E, F#, G, A, B, C#, D. However in just intonation, the “Type A” scale produces a perfectly tuned E minor chords but an out of tune A major chord, whereas in the “Type B” scale this is the other way around (a perfectly tuned A major chord but an out of tune E minor chord). Which scale works best in a given context is determined by the melodic material and harmonic progression of the musical piece. This makes diatonic music in just intonation both more complicated and less flexible than in equal temperament. However, the advantage is that it results in a degree of “in-tune-ness” and harmonic resonance that is simply not attainable in 12 tone equal temperament. Scales with the “Type A” or “Type B” shape have what I would call ‘maximum harmonicity’. Each of these scales accommodates 5 different perfectly tuned triads and this is the highest number possible for a diatonic scale. In the case of Ionian Type A, these chord are: I major, II minor, III minor, IV major, VI minor. In the case of Ionian type B they are: I major, III minor, IV major, V major, VI minor. The other scale shapes (Type C-F) all have less well tuned chords contained within them, yet these shapes are important too, because they map to many common chord progressions that don’t fit with the A or B types. In the illustration above, the types C through F all produce Dorian scales, each accommodating different chord progressions. For example, to match the chord progression I minor – IV major, bVII major, we would need to use the “Type D” scale.
I have used these – and other – scale types to create a selection of 21 diatonic scales on the Arithmophone Korale. They are shown below here in diagram form.

For pentatonic scales, there isn’t really a generally accepted naming convention, so I decided to get a little creative myself:

In Western music, there are only two common pentatonic scales (known simply as ‘minor pentatonic’ and ‘major pentatonic’). I labeled the shapes that produce these scales “Occident”. Two other shapes that I recognised form Ethiopian and Japanese music, I labeled “Orient”. Then I found two more shapes I wanted to use because I liked their sound, even though I didn’t really recognise them from any musical tradition that I’m familiar with. I labeled these “Mirror” because they form the mirror image of the “Orient” shapes. Since each of these shapes comes in two versions (which are in fact a 180 degree rotation of each other), I used the terms “Sun” and “Moon” to distinguish these. This is closely related to the distinction between major (Sun) and minor (moon), but since pentatonic scales don’t always contain a third and are therefore sometimes neither major nor minor, strictly speaking, I decided that a separate term was warranted. To further distinguish different scales, I also used the letters O for ‘Overtonal’ and U for ‘Undertonal’, depending on the positioning of the 1/1 ratio within the shape. Because I wanted each pentatonic scale to be a subset of the corresponding diatonic scale, some overlap was hard to avoid, resulting in a selection of 19 different pentatonic scales:

I hope this article explains some of the workings of the different Arithmophone keyboard styles and that it will encourage you to play around with them and experiment freely. If you have any feedback, corrections or suggestions, please let me know!
This page is part of my Arithmophone project.
Arithmophone concept and design by Chiel Zwinkels © 2023
