*** This page refers to a legacy version of the Arithmophone. The latest version can be found here ***
The Arithmophone is a virtual keyboard instrument. To play it, simply touch the keys – or click on them if you don’t have a touchscreen.
The Arithmophone features 5 different keyboard styles. Most of these keyboards have notes that are a little different from the notes on a regular piano keyboard. On a standard piano, there are 12 notes in each octave, and these notes are all the same distance apart. The distance between any note and the next is exactly one twelfth of an octave. This kind of tuning is called ‘12 tone equal temperament’. It is also known simply as ‘standard tuning’, because it has become the standard tuning scheme for most Western music, both acoustic and electronic.
However, there are many other ways to tune an instrument. On the Arithmophone, only the ‘ToneBrick 12’ keyboard style uses the notes of 12 tone equal temperament. The other keyboard styles use different tuning schemes and each of these has its own sonic signature. In fact, one of the purposes of the Arithmophone is to encourage you to explore these alternatives to the standard tuning system, in an environment where they can easily be compared side by side.
The settings menu
By pressing or clicking the button in the top right corner, you can open the settings menu. The first options let you select the keyboard style: the Arithmophone comes in five different flavours. I will give a brief and very subjective description of each of the styles here. A more detailed description of each style, along with illustrations that show which key does what is provided later in this manual.
- The Junior is the simplest keyboard style provided. It is intended to be as accessible as possible, both in terms of the screen size required and of the musical experience of the player. It features a selection of notes in 5-limit just intonation tuning, which makes for very warm and grounded harmonies. Its sound is both comfortably familiar (because it uses all the most elementary harmonic relations) and slightly exotic (because so much of Western music uses tempered tuning instead of just intonation).
- The ToneDiamond also features just intonation tuning in a 5-limit system, but in a different form factor. It uses mostly the same notes as the Junior and shares its sonic signature, but provides a larger range. It splits each square into two keys, which provide different octaves of the same note. This gives it a complete two octave range with certain important notes also available an octave above and below.
- The ToneHive get its name from its hexagonal keys. It also uses just intonation, but extends it to a 7-limit system. It splits each hexagon into three keys, providing more octaves per note for a full three octave range. It offers the same familiar notes as the Junior and the ToneDiamond, but adds to these the much less familiar sound of notes from the realm of septimal harmony.
- The ToneBrick 12 uses the familiar tuning of 12 tone equal temperament (the same as used on regular pianos, guitars et cetera) but in a much less familiar layout. Because this is an equal tempered tuning, there is no one note that is more central than any other, and this is reflected in the shape of this keyboard. It is not built around a single center, but constructed as an equal grid. Only in the colouring is there a ‘favoured’ note, but this is mainly to help with navigation of the grid. The sonic character is subtly different from the equal tempered keyboard styles: not quite as grounded, with a certain sense of being permanently afloat. Unlike in just intonation, there is no true ‘home’ key in equal tempered tuning.The way the notes are arranged accentuates this property: patterns can be played anywhere on the keyboard and will always produce the same harmonies, only from a lower or higher starting point. The smaller version of the ToneBrick 12 uses double octave keys for a three octave range, the larger version uses quadruple octave keys for a full five octave range.
- The ToneBrick 31 also uses a tempered tuning system, but this time the much less common 31 tone equal temperament, which features 31 notes to the octave instead of the common 12. These notes are very close together and can easily appear to be out of tune versions of the same note, making this keyboard the most difficult to navigate. But it also provides very accurate approximations of many just intonation intervals while still retaining all the harmonic flexibility of a tempered system. The smaller version of the ToneBrick 31 uses double octave keys for a two octave range, the larger version uses quadruple octave keys for a full four octave range.
The other options in the settings menu makes it possible to change the pitch and sound quality of the notes themselves.
- The oscillator type buttons allow you to adjust the basic waveform from a pure sine wave (no harmonics: dark and bassy) to a square wave (lots of harmonics: bright and trebly).
- The first slider controls the frequency of the central note. It defaults to 392 Hertz, which is equal to the note G4 in standard tuning. It can be raised or lowered by a full octave or any smaller interval (in steps of 4 Hertz).
- The brightness slider allows you to roll of some high frequencies. This can help make the sound more pleasant on small speakers (like the built-in speakers of a phone or tablet).
- The attack and release sliders control the way the volume of each note changes over time. The attack time determines how fast the note rises to its maximum level and the decay time determines how long it rings out.
- The tremolo and reverb sliders control the built in effects. These are included to make the sound a little more lively, the tremolo by varying the overall volume and the reverb by making it more spacious.
Please note: the following sections assume a basic understanding of musical notes and intervals, just intonation ratios and temperaments. If you are unfamiliar with these things, everything you need to know is in this interactive guide to the building blocks of melody and harmony.
The basic structure of the keyboards
On a standard piano keyboard, the notes are arranged from low to high (going from left to right). Although the keyboard itself is a 3-dimensional thing, with its raised black keys, this layout is basically one-dimensional: all the notes are arranged along a single line.
The Arithmophone on the other hand, uses a two-dimensional grid. Arranging the notes in two dimensions instead of one has some interesting advantages, especially for an on-screen keyboard: it can help to make the relationship between different notes more intuitive, make many chords and melodies easier to play and it also makes more efficient use of the available space on the screen.
When we arrange the notes in two dimensions, it no longer makes sense to order them simply from lowest to highest, so we need to find some other way of arranging them. We can start by selecting some ratio, for example 3/1, and placing the same ratio between each pair of adjacent notes, like this:

These numbers represent the ratios of the frequencies: if the 1/1 note has a frequency of 100 Hertz, then the 3/1 note is 300 Hertz (3*100), et cetera. Each note has a frequency that is three times as high as the note to the left of it. In terms of standard note names, taking C as the central note, this example looks as follows:

Once we have this first row of notes, we can chose a different ratio, for example 5/1, for the notes above and below, like such:
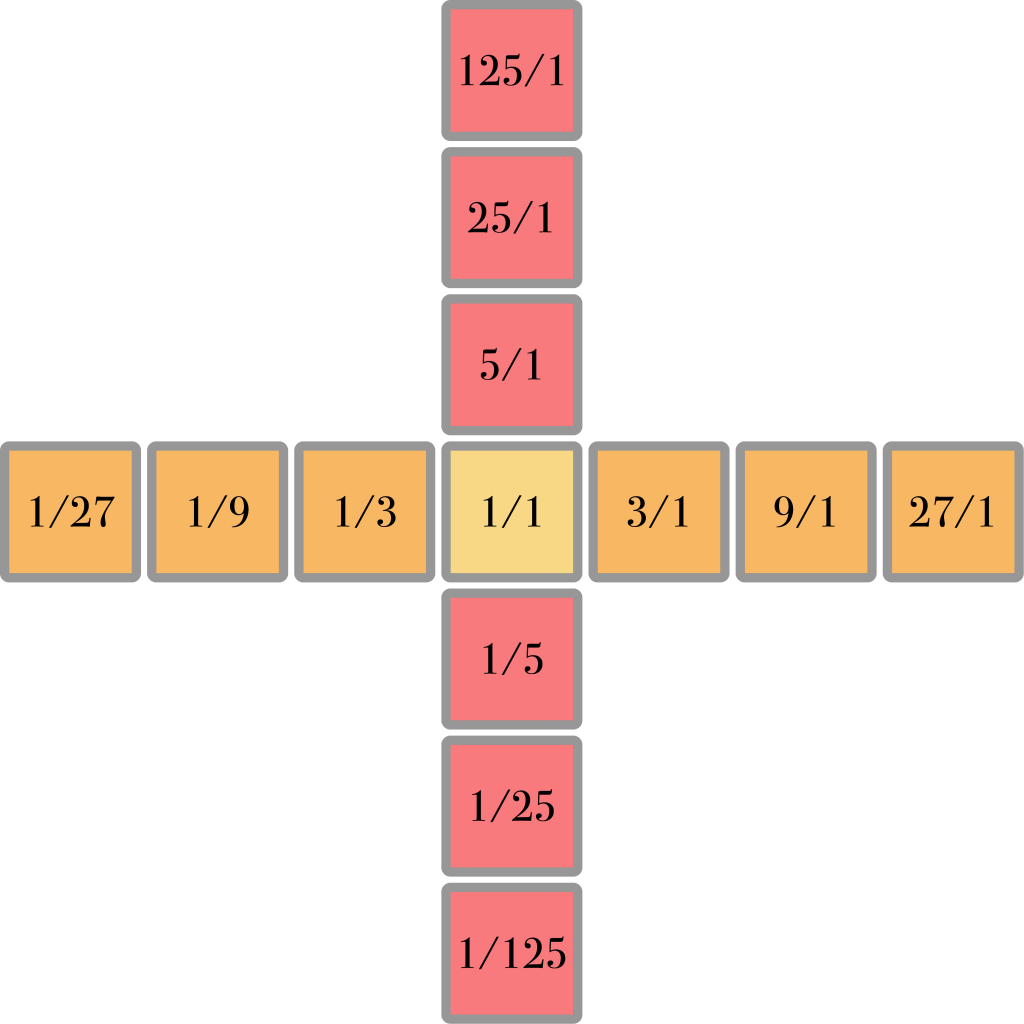
With note names instead of ratios it now looks like this:
By filling out the other columns we can make a grid like this:
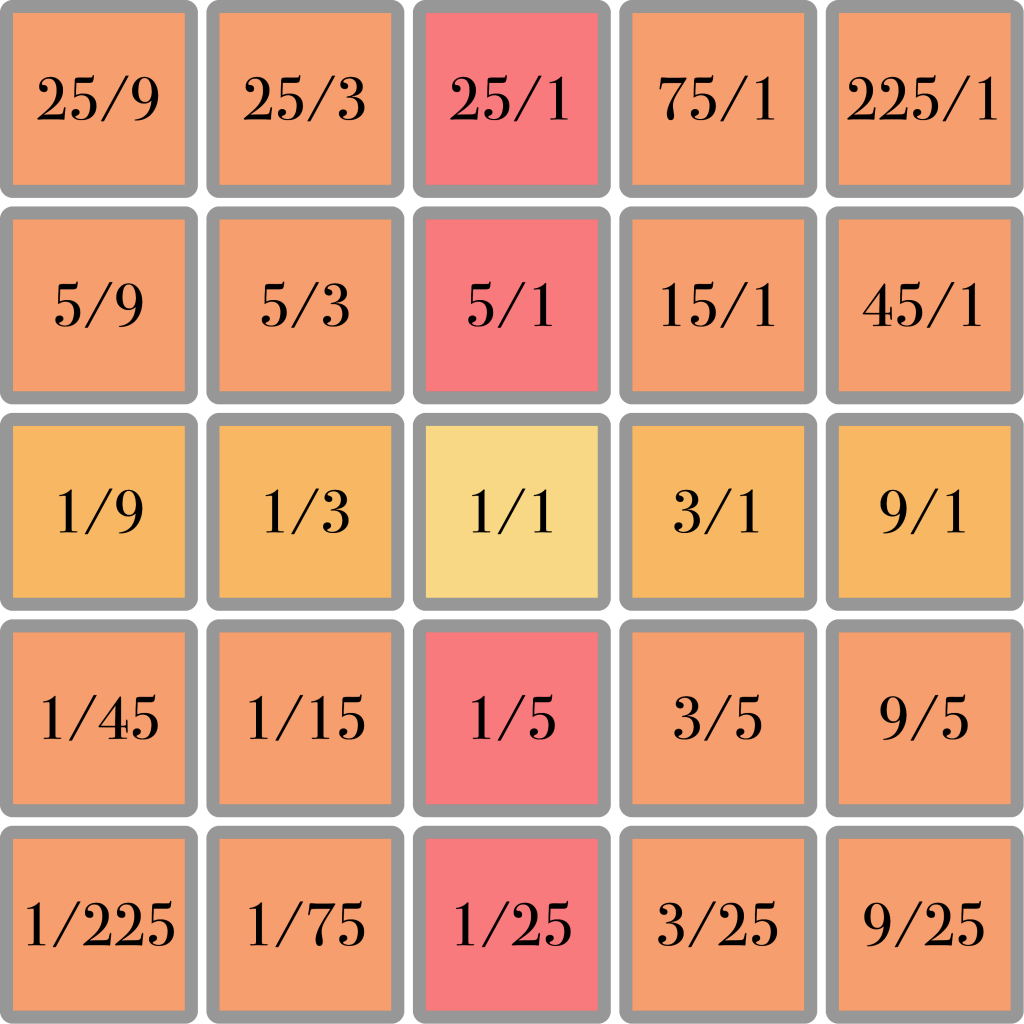
This is how many musically useful intervals arise. The ratio 3/5 does not appear as a direct over- or undertone of the 1/1 note, but it is present in the harmonic spine of the 3/1 note and in this way it is strongly (though indirectly) related to the 1/1 as well. 3/5 is in fact the note known as the just minor third, an very common note in almost any kind of music.
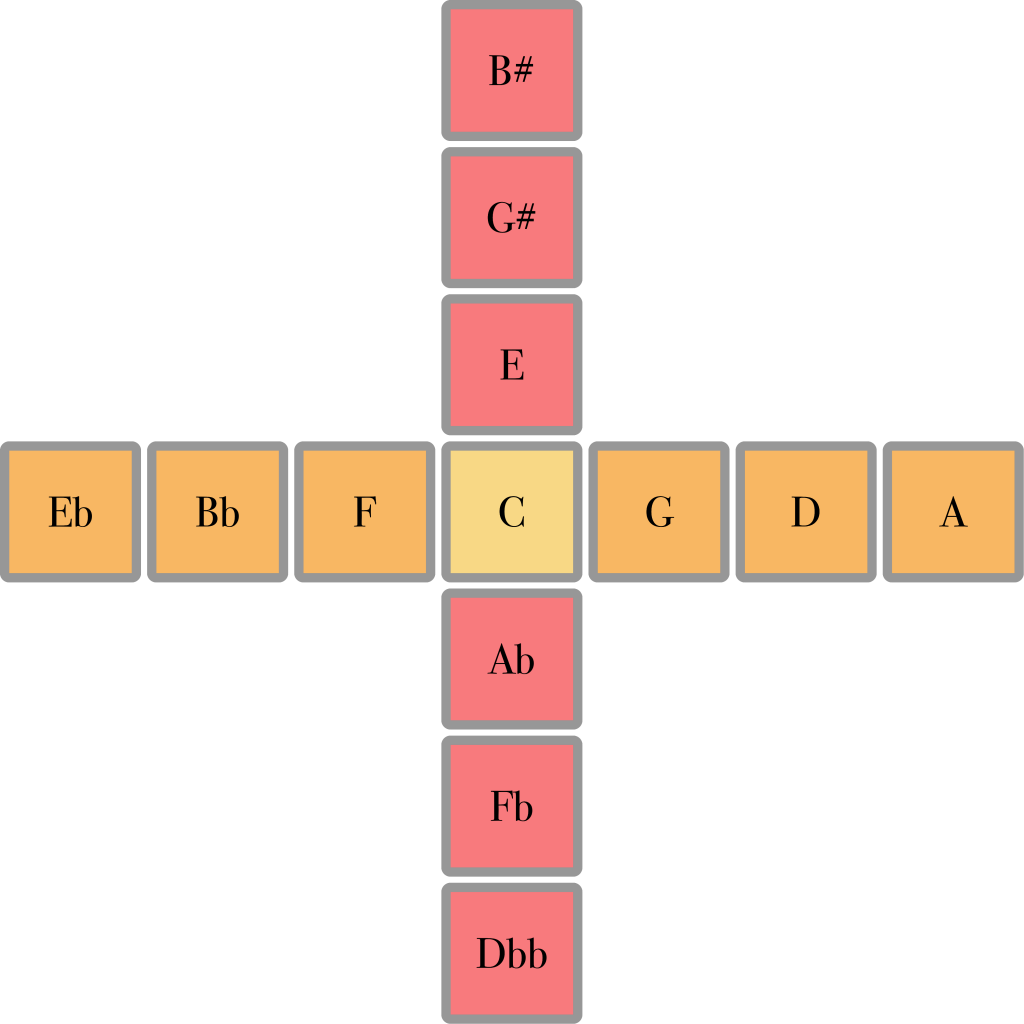
With note names instead of ratios, it looks like this:
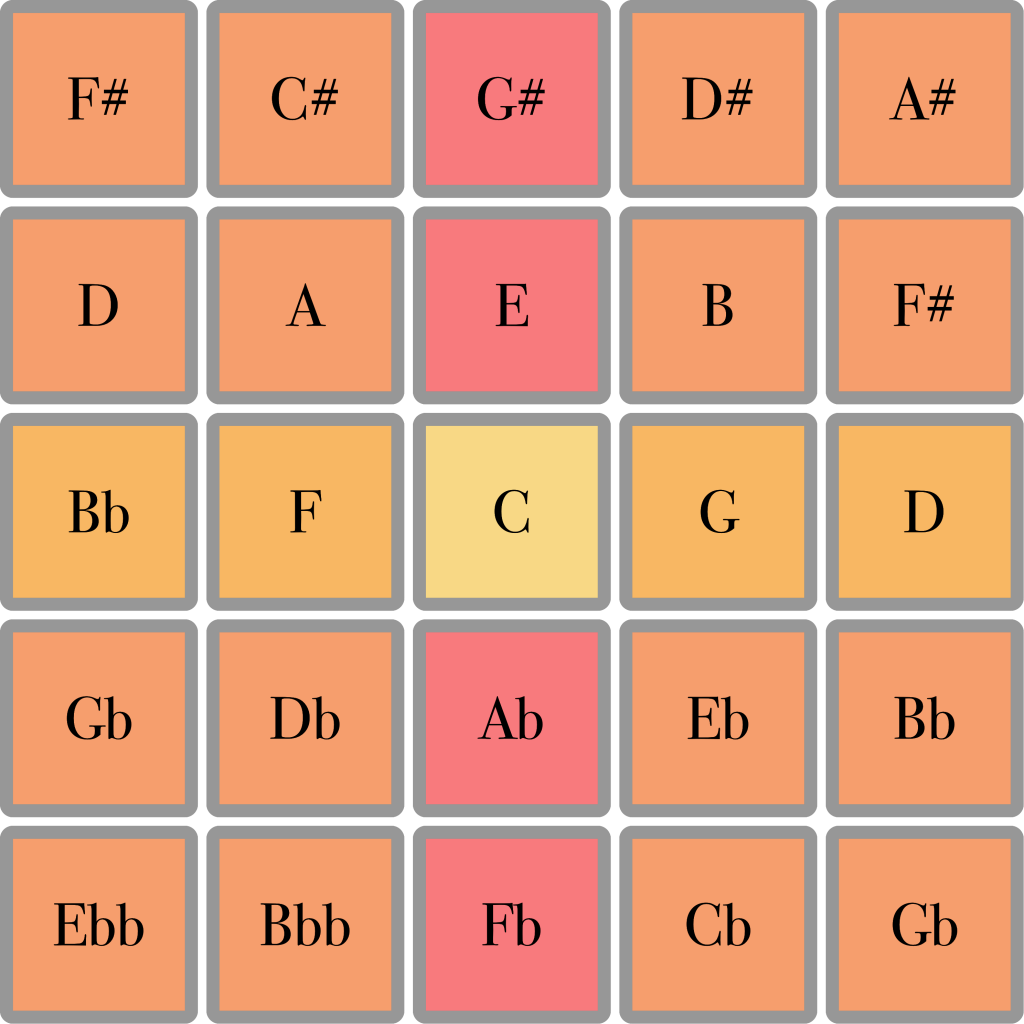
This type of keyboard layout is called isomorphic. This means that wherever you are on the keyboard, moving a certain step always results in the same musical interval. In this example, if you move one step up, you always get a major third, et cetera. Unlike on a piano, once you have learned a certain pattern, chord or melody in one key, you can play it in any other key just as easily.
In standard tuning, this pattern starts repeating pretty quickly, because many keys with different note names are actually the same note. On a piano, G# and Ab for example, are really just different names for the same key. In just intonation, this is not the case, and each key has its own note. G# is a different note from Ab, and even the two Bb’s in the grid above, although they have exactly the same name, are actually different notes.
This kind of isomorphic grid works very well for tempered tunings, and in the Arithmophone, variations of this layout are used for the ToneBrick 12 (12 tone equal temperament) and ToneBrick 31 (31 tone equal temperament) keyboard styles. It does not work so well for just intonation keyboard, because there it generates infinitely many different notes, many of which are not very relevant musically speaking. So for the just intonation keyboard styles, ToneHive and ToneDiamond, a different approach was needed.
Those keyboards are based on what I call ‘harmonic spines’. A harmonic spine is a set of notes that are directly under- and overtonal to a central note. A basic harmonic spine looks like this:

This spine contains all overtones and undertones of the central 1/1 note up to the seventh harmonic. It could be extended further in both directions, to include the ninth harmonic, the eleventh harmonic et cetera.
Only odd numbers are included, because even numbers don’t introduce any new notes. Those are simply octaves above and below existing notes: 6/1 is an octave above 3/1 and so on. The 1/1 note forms the center of the keyboard, but a harmonic spine does not have to start on the this note, it can be constructed from any note. The example below shows a secondary harmonic spine starting on the 3/1 note.
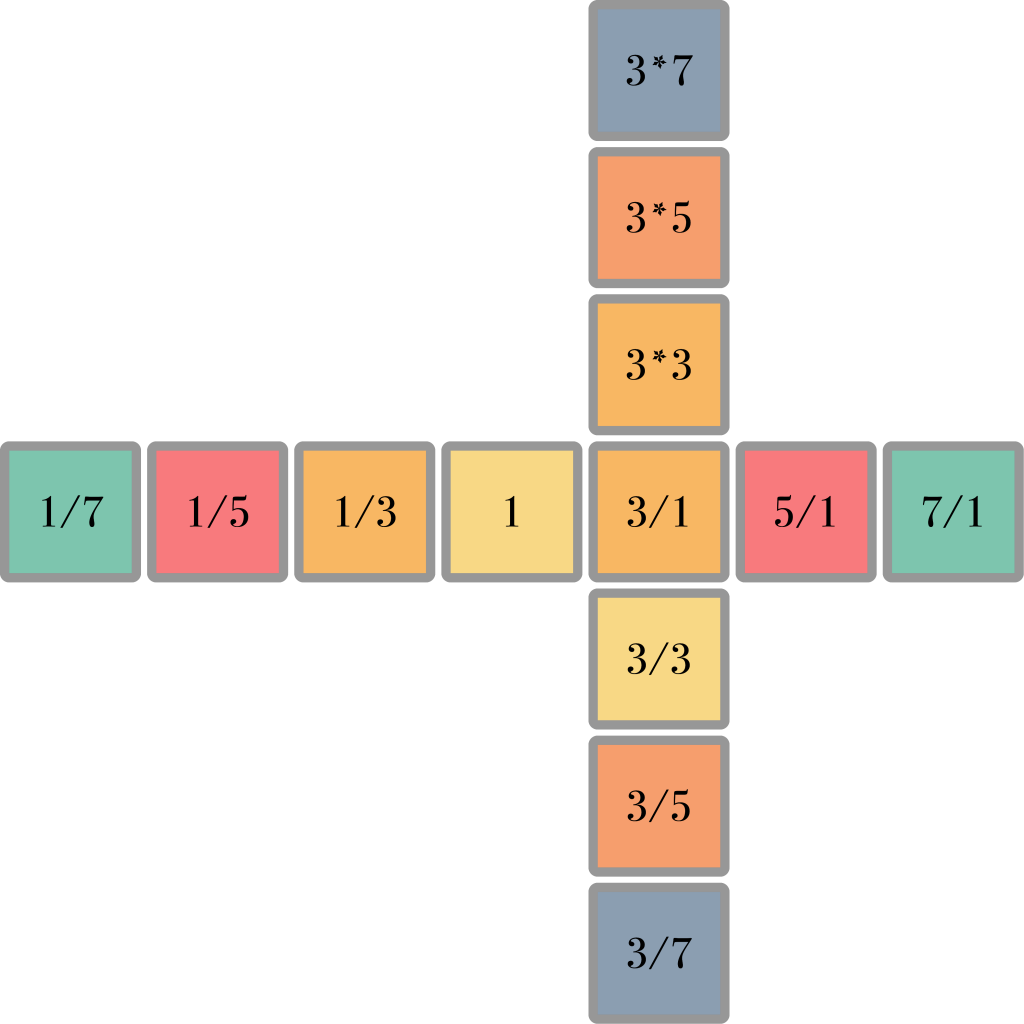
When we extend this principle and use it to make a square of harmonic spines, we obtain many of the most common musical intervals:
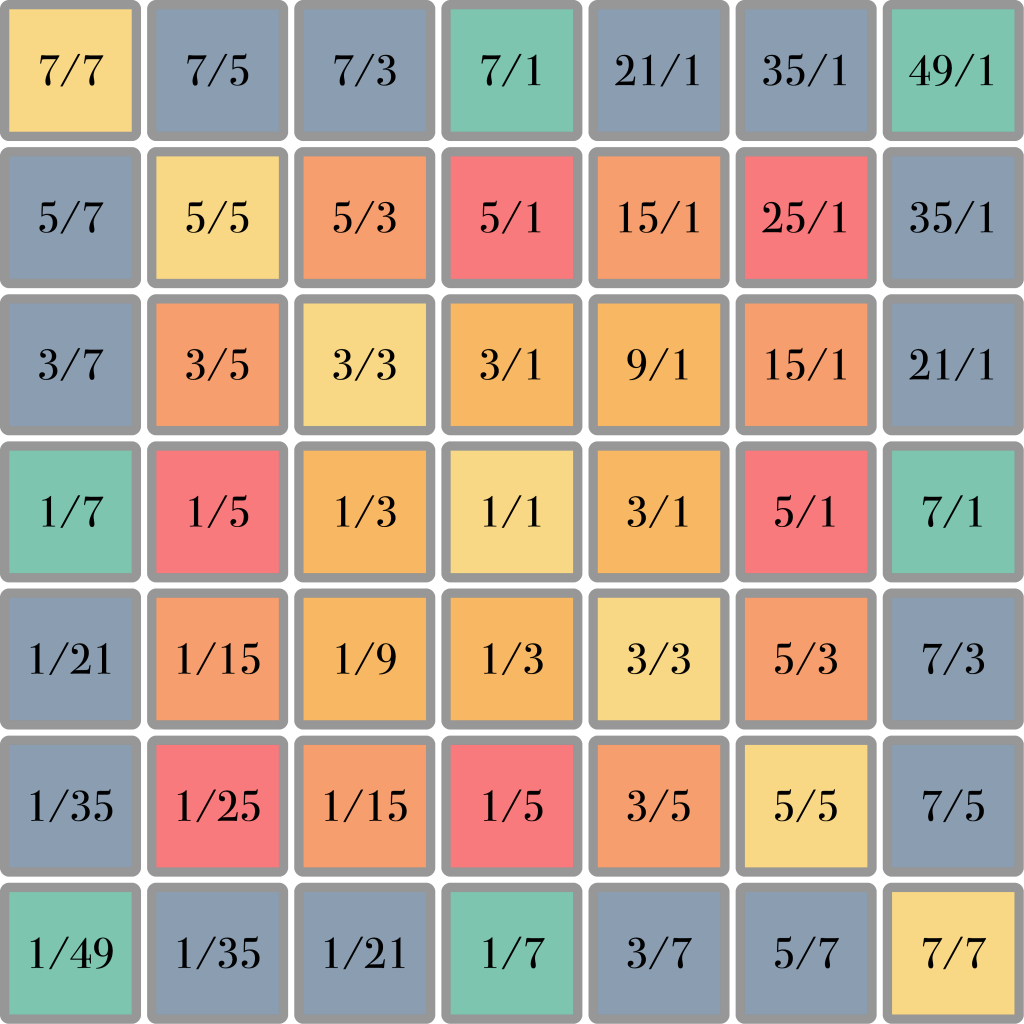
However, as a musical keyboard this layout is not very efficient. It generates a lot of duplicates: the same ratios appearing in different places. To remedy this problem, we start by folding the central harmonic spine around the 1/1 ratio like this:
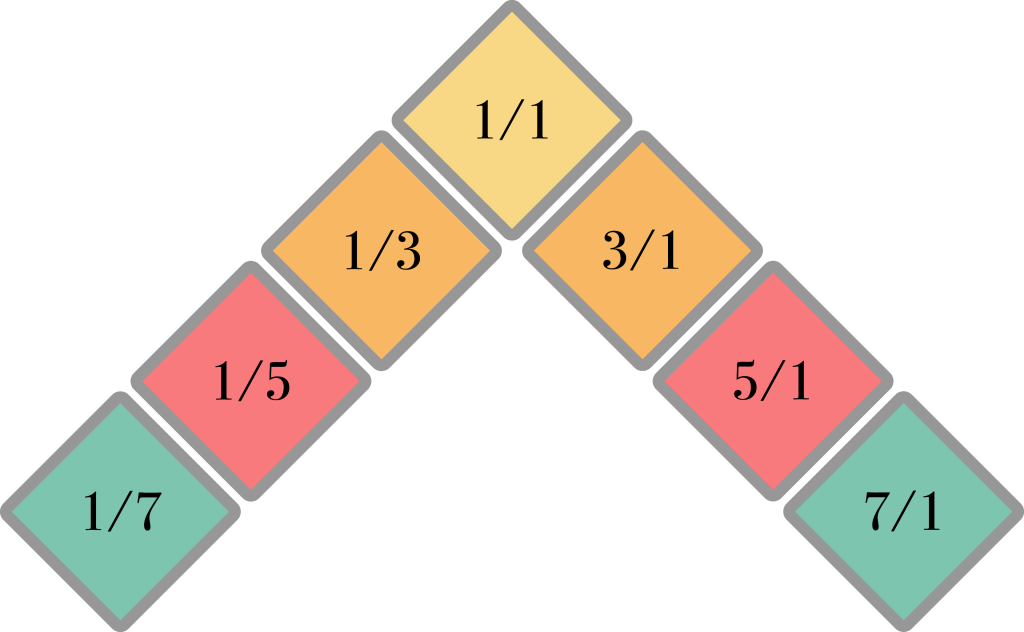
If we start filling in the secondary harmonic spines now, we will see that most of the duplicates land in the same place and therefore become a single key. First we fill in the spines in the inward direction:
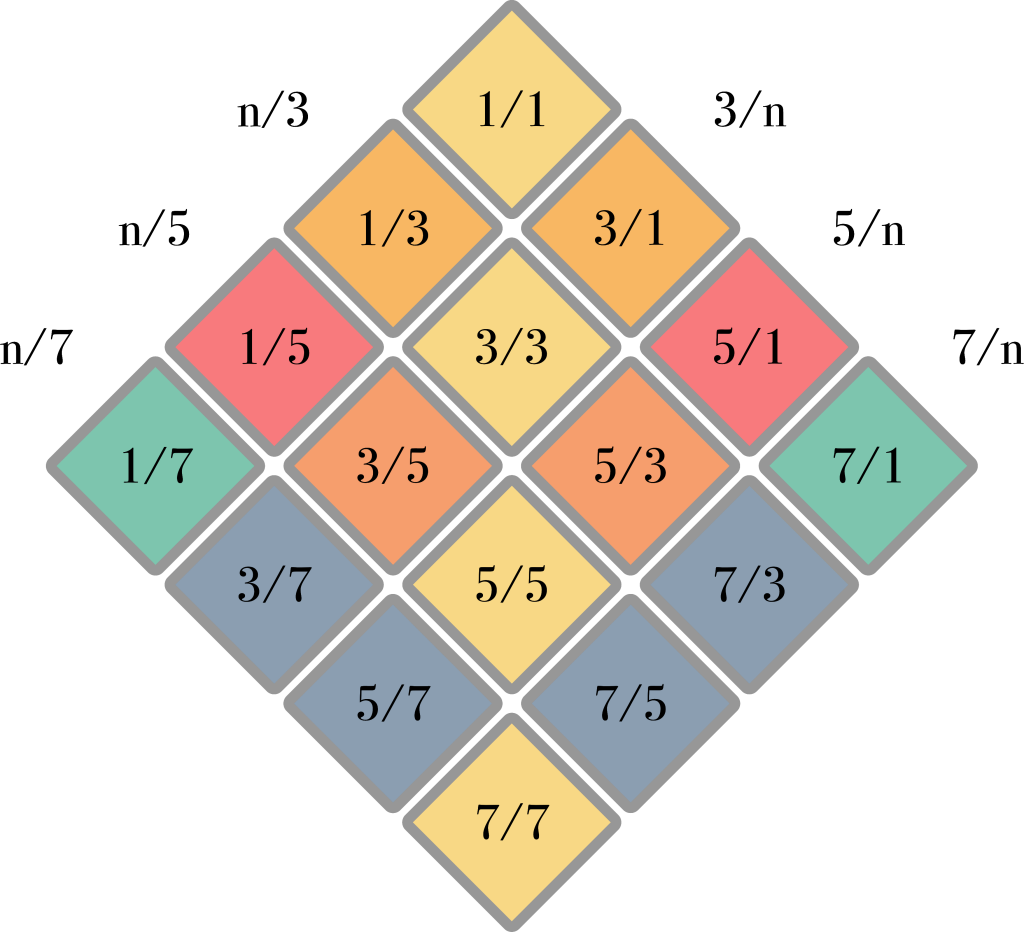
And then we complete it in the outward direction:
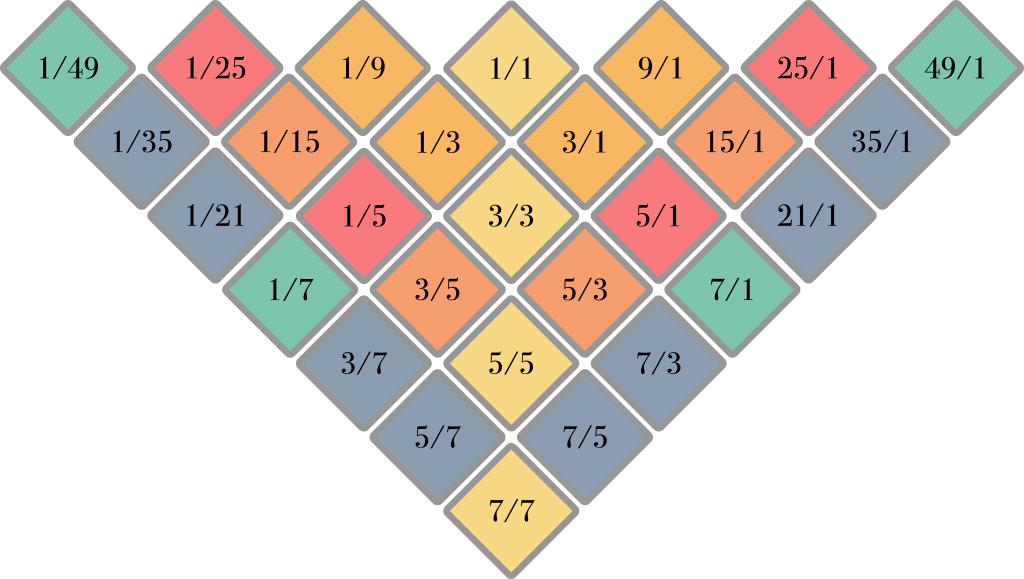
Now we have all the same intervals as in the square layout, but we only need slightly more than half the keys. This intertwining of harmonic spines forms the basic harmonic structure of the ToneHive and ToneDiamond keyboard styles.
Keys and colours
On the Arithmophone, the colours of the keys reflect the nature of the interval they form with the central note. For the just intonation keyboards, this represents an exact relationship. For the tempered keyboards, the relationship is only approximate, but the colours nevertheless provide a helpful means of navigating the different notes. The basic colouring works as follows:
- Light yellow is used for the central note (the 1/1 ratio) and its higher and lower octaves (4/1, 2/1, 1/2 and 1/4)
- Dark yellow is used for notes in pure 3-ratios, such as 3/1 and 1/9
- Red is used for notes in pure 5-ratios, such as 5/1 and 1/25
- Orange is used for notes in combined ratios of 3 and 5, such as 5/3 and 1/15
- Blue is used for notes in pure 7-ratios: 7/1 and 1/7
- Bluish green is used for notes in combined ratios of 3 and 7, such as 21/1 and 3/7
- Green is used for notes in combined ratios of 5 and 7, such as 35/1 and 7/5
- A second shade of bluish green is used for notes in combined ratios of 3 and 5 and 7, such as 63/5 and 9/35
In the ‘ToneBrick 12’ keyboard style, pinkish orange is used for the II and bVII notes: although these are best approximated by the pure 9/1 and 1/9 ratios respectively, they are functionally just as likely to stand for the combined 5/9 and 9/5 ratios in 12 tone equal temperament. I felt this ambiguity justified another colour, especially because this also made the layout a little clearer. In the ‘ToneBrick 31’ keyboard style, blue is used for all ratios containing a 7; bluish green and green are instead used for notes that approximate the 11th and 13th harmonics.
There is a meaningful connection between the colours of the keys and the “sound colours” of the notes they produce, in relation to the central note. It is not a straightforward one, but I hope it will reveal itself by playing around with the Arithmophone, and provide some insight and inspiration along the way.
If the explanation above sounds a bit abstract to you, I would like to recommend once more my introductory guide to the building blocks of melody and harmony.
Unlike on most instruments, the distance between notes on the Arithmophone does not correspond to their distance in pitch, but to their harmonic distance. The simplest harmonic interval is the octave, and different octaves of the same note are bundled together in groups of 2, 3 or 4 (except in the ‘Junior’ keyboard style, which uses single octave buttons).
Intervals that are mainly overtonal (formed by multiplication) are on the right hand side of the keyboard, and intervals that are mainly undertonal (formed by division) are on the left hand side. This symmetry between overtones and undertones is also very important in music, and I hope that the layout of the Arithmophone can help to illuminate this fact. Try playing a simple pattern that moves from left to right across the center of the keyboard, then playing the mirror-image of that pattern from right to left, and listening for the way these patterns relate to each other.
The Junior
The Arithmophone Junior is the simplest keyboard style available, and it is specifically designed to be useable on smaller devices like phones. It uses just intonation tuning in a 5-limit system. In this system, only ratios that are built out of the prime numbers up to 5 are used. This may seem very limiting, but in this way we can already produce all the notes of the standard Western tuning system, and many more as well.
Because 5 is the highest prime factor allowed in this system, the spines do not feature any ratios containing a 7 or higher. After 5, the next smallest possibility is 9 (3*3), then 15 (3*5) and then 25 (5*5).
Forming the central spine in this way and then filling in the secondary spines gives the following map (the central spine is indicated with grey borders):
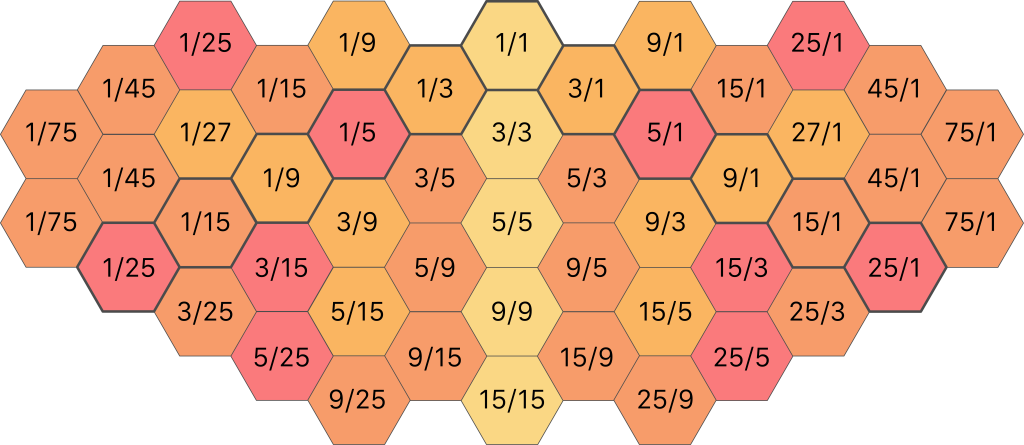
Many of these ratios are actually the same value, for example 15/5 is the same thing as 3/1. After simplifying where possible, the map looks like this:
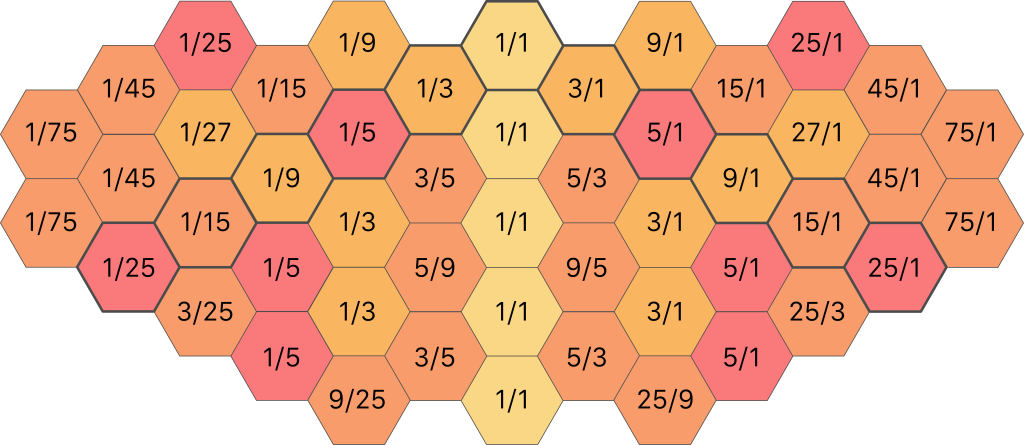
Now, we have quite a few doubles. We can use this to our advantage by making these notes available across different octaves. After doing this, and using octave reduction to bring all the notes within the same range, the final ratios that are actually used in this style are as follows:
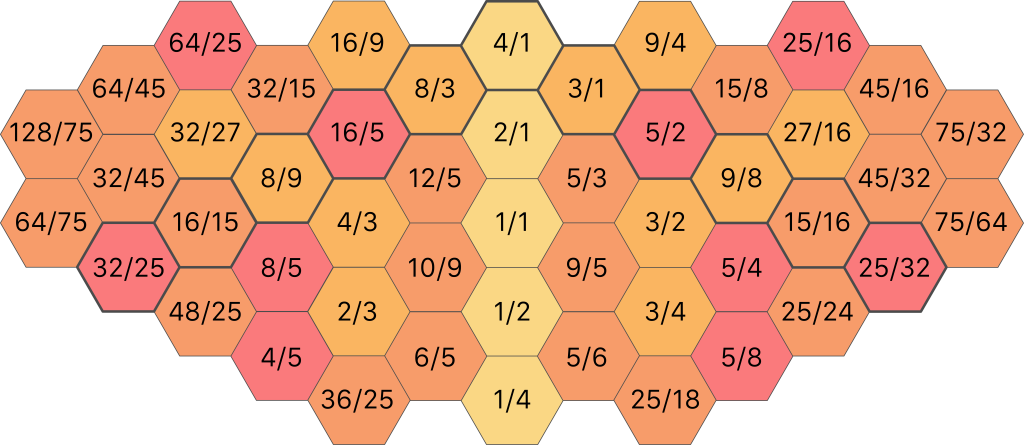
That is a lot of numbers, and although this is the most accurate representation of the pitches used in the ToneHive 5, it may not be the most helpful for finding your way around on it. Below is another illustration, this time with note names instead of ratios. This is a lot easier on the eye, but one very important thing should be kept in mind. In the world of just intonation, F# does not equal Gb: these notes are close in pitch, but not identical. Also, some notes that do have the same name appear in different versions. For example, 5/3 is represented by the note name E (up a third from G to B, then down a perfect fifth from B to E), but so is 27/1 (up a fifth from G to D, up another fifth from D to A, then up one more fifth from A to E). These too are close in pitch but not identical. So there are two different E’s. Such notes are distinguished in this illustration by a + or – sign after the note name.
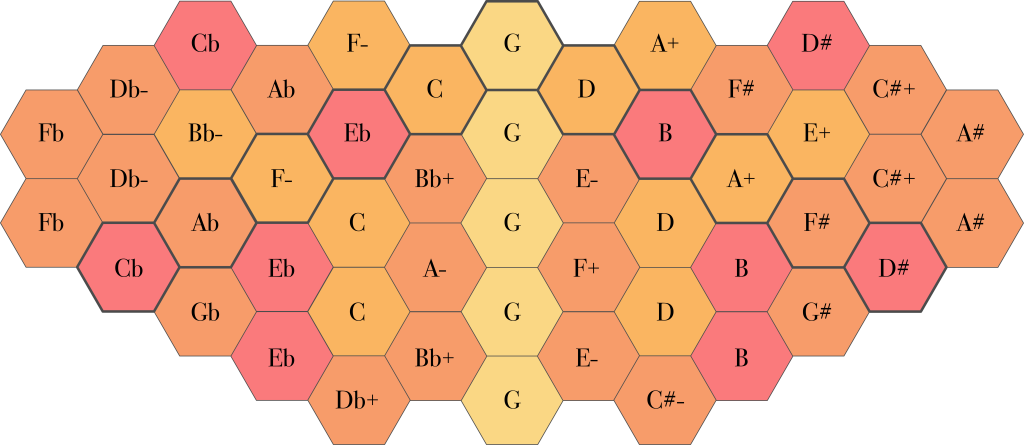
Of course, you can change the center frequency to any note you like, and all the other notes will move along with it. In that case, the note names in the illustration above are no longer applicable. For the sake of completeness, I include a more general illustration with scale degrees instead of note names:

The ToneDiamond 5
The ToneDiamond style offers much the same notes as the Junior, but uses a somewhat different layout. Its proportions and larger number of keys make it more suitable for square-ish, tablet sized screens. Both the Junior and the ToneDiamond offer 25 different notes altogether, but the different shape of the keyboards does result in one difference in the note selection: whereas the Junior features the 25/9 and 9/25 ratios, the ToneDiamond omits these in favour of the 125/1 and 1/125 ratios. Written in simple form, these are the ratios used on the ToneDiamond:
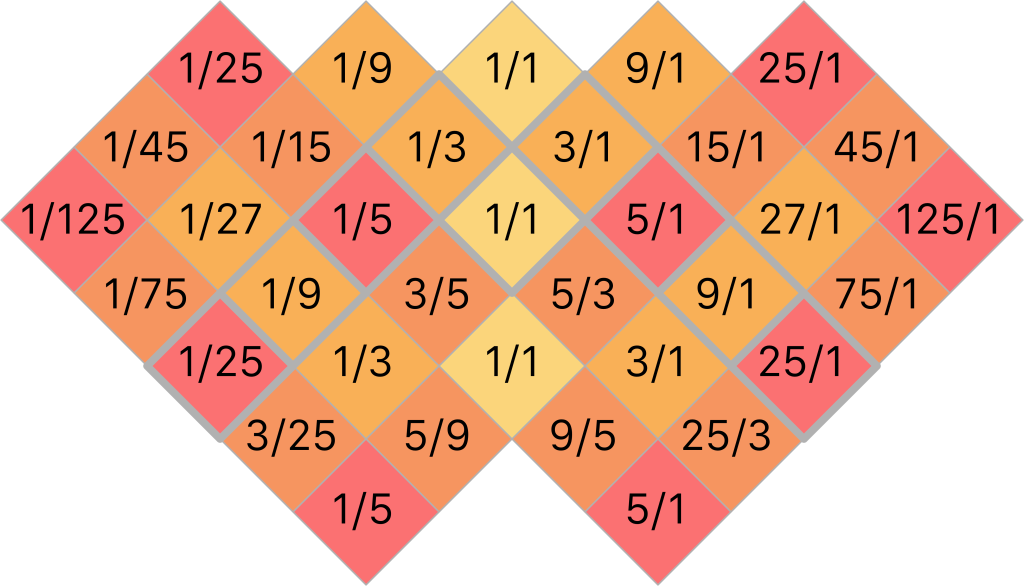
The ToneDiamond introduces another important feature of the Arithmophone: grouped octaves. Whereas each hexagon on the Arithmophone Junior is just a single key, on the ToneDiamond each square is split up into two keys. These keys both produce the same note, but in different octaves. For example, the square labeled ‘3/5’ in the illustration below, contains keys for 3/5 and 6/5. Because multiple octaves are now available on each note, it becomes less desirable to have recurring notes in the plan. For this reason, the 15/1 and 1/15 ratios, which do not introduce any new notes in their secondary spines, are skipped over in the central spine. These are the note names of the ToneDiamond:
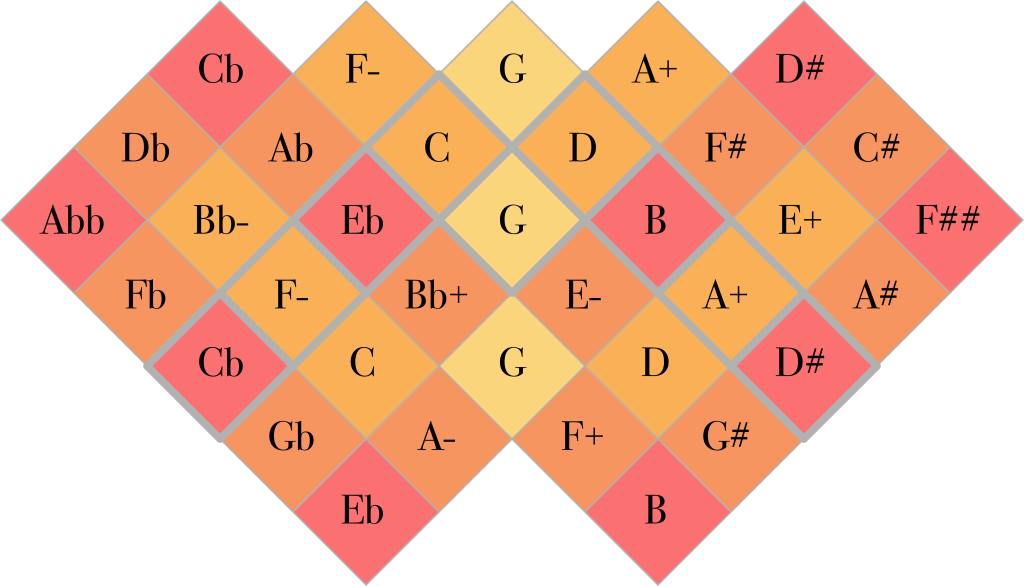
And finally, once more the scale degrees:
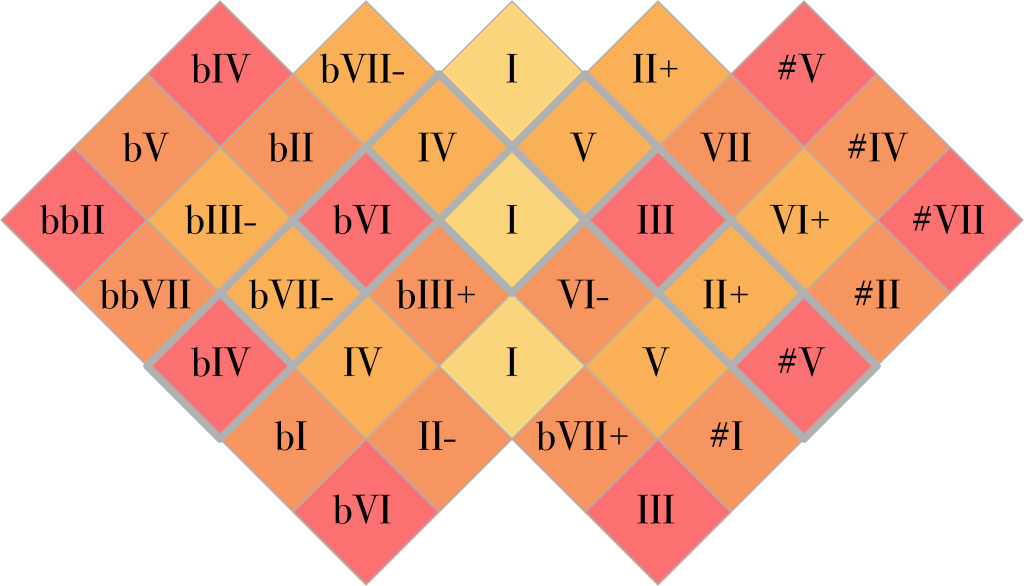
The ToneHive
The ToneHive keyboard style also uses just intonation, but extends the prime number limit from 5 to 7. This introduces a whole new class of notes, that are not really represented in the standard Western tuning system, although they do appear frequently in Blues and Jazz, at least on instruments with flexible tuning like slide guitars and saxophones (and of course in singing). These notes are often referred to as ‘blue notes’, a fact I have represented in the colour scheme of this keyboard style.
Some notes with 7-ratios are extremely close in pitch to notes with 5-limit ratios, for example 7/5 and 45/1. After octave reduction, the interval between these notes is only 225/224, very close to 1/1 (if the interval were exactly one, that would mean they were the same note). These notes are almmost interchangeable. For example, if we start on 9/1 and want to add a major third above, we would normally use 45/1 (because 9*5 is 45). But if we use 7/5 instead, we still hear a very convincing major third. In fact, it is much more accurate than the major third we are used to in standard tuning: whereas the major third on a well tempered piano deviates from the pure 5 ratio by about 14 cents, this switch between 45/1 and 7/5 results in a deviation of only 7 cents (a cent is 1/1200 of an octave, or 1% of a standard semitone).
The ToneHive layout is based on harmonic spines just like the Junior and the ToneHive. However, in order to create an interesting and coherent selection of notes, I have taken quite a few liberties with the basic structure in this case. The harmonic spine is only followed up to the 7th harmonic, multiples like 9 and 25 don’t get their own spine anymore. Instead, I have created a ring of notes around each of the intervals 7/1 and 1/7, coloured in shades of blue and green, filled out with a few remaining 5-limit notes that don’t appear in the basic spines but are still very relevant in a musical context.
In basic ratios, the final result is as follows (the shortened central spine is indicated with grey borders):
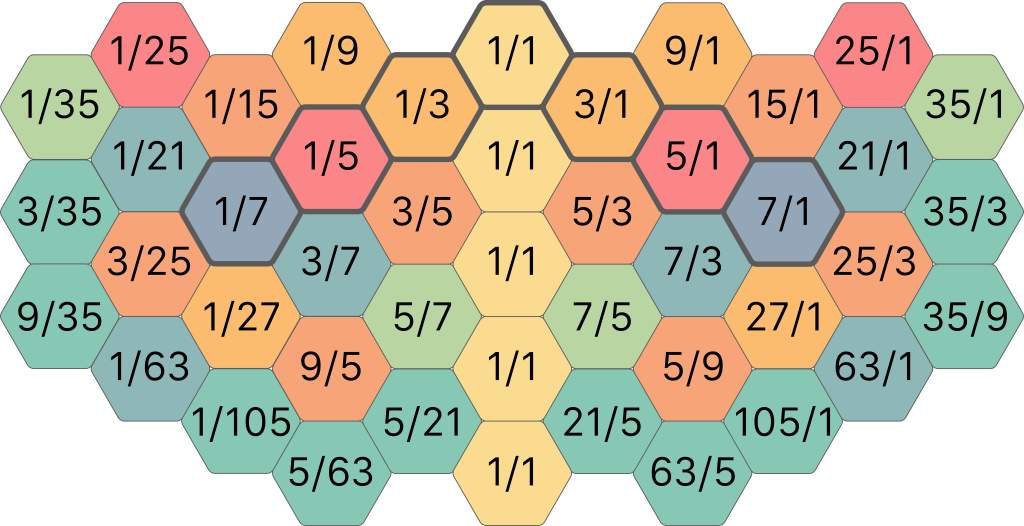
This makes for three different areas: the notes in yellow, orange and red are all centered around the 1/1. The blue and green notes on the left are centered around 1/7 and form their own coherent set of chords and scales. The same thing applies to the blue and green notes on the right, only those are centered around 7/1. These areas are connected in two different ways: by a direct leap of 7/1 or 1/7, but also by the close connections created by the 225/224 exchange.
In the 7-limit system, the mapping of ratios to note names becomes difficult. It should be remembered that note names and scale degrees are only labels, ones that work quite well for 5-limit just intonation (and for 12 tone equal temperament), but not so much for other tuning systems.
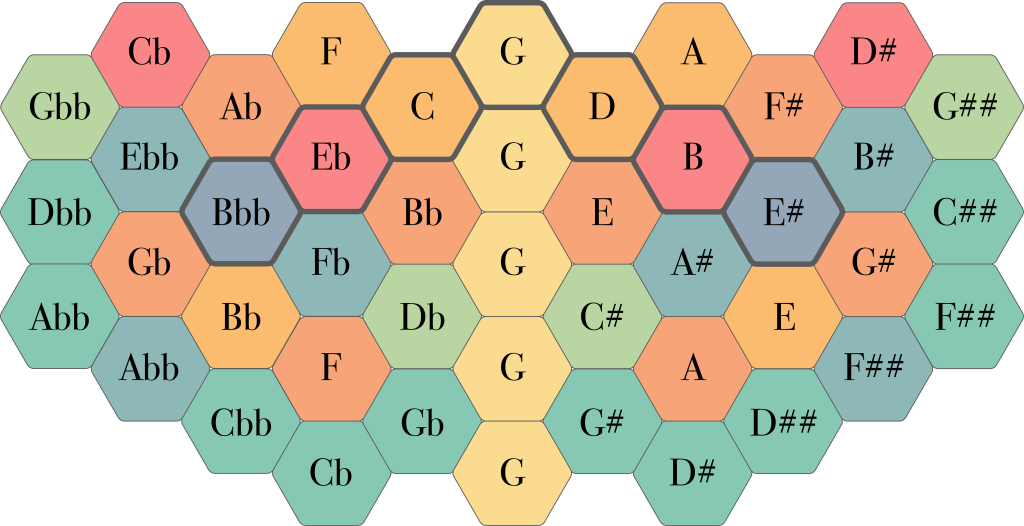
Still, because the illustration above is rather difficult to read, I do provide the version below for easier reference. However, please keep in mind that note names are used very loosely here and that notes sharing the same name can be wildly out of tune from each other. I’ve found that in the 7-limit system, it is best to get to know each note for what it is of itself, and forget about the standard nomenclature as much as possible.
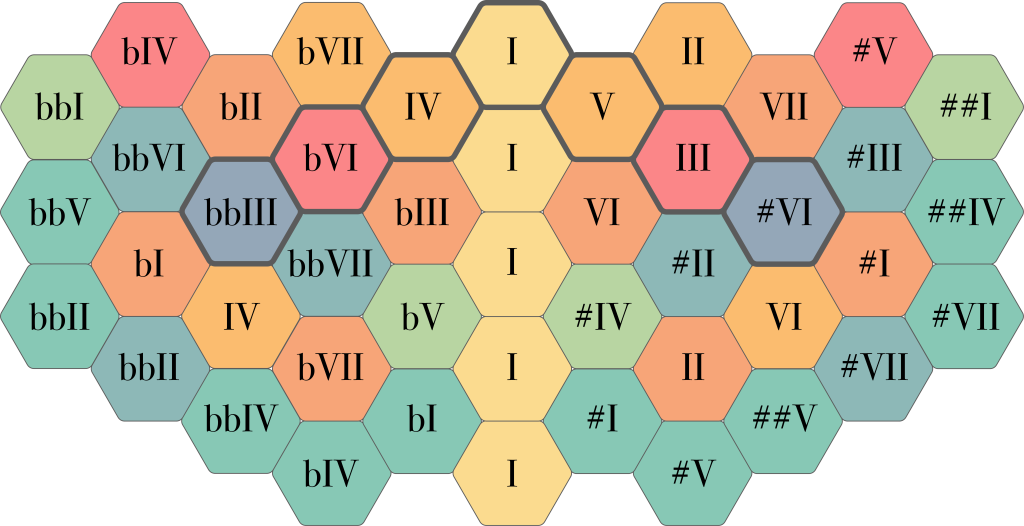
And finally, once again just for reference, here is another map of the ToneHive, showing the approximate scale degrees. Just like the note names above, these should be taken with a grain of salt.
The ToneBrick 12
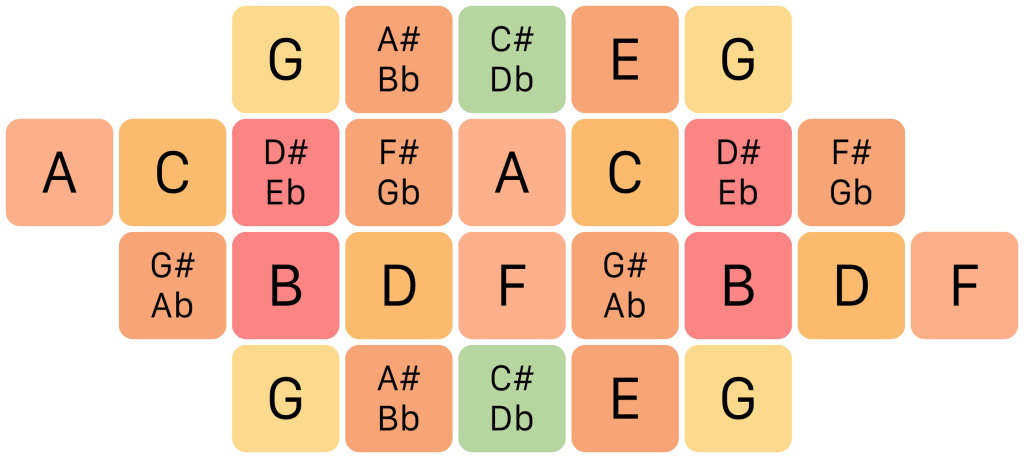
The ToneBrick 12 style takes a very different approach from the Junior, ToneHive and ToneDiamond styles. It uses the familiar notes of 12 tone equal temperament (the standard piano notes), but laid out in an isomorphic grid. Every horizontal step results in a minor third and every vertical step in a major third. To be clear, these are tempered thirds, not the perfect thirds of just intonation. Because this is an isomorphic grid, the same shape played anywhere on the keyboard will always produce the same harmonic pattern. For example, starting on any note, going up one square and then right one square will always produce a major triad. This accentuates the free-floating nature of equal tempered tuning: unlike in just intonation, there is no true ‘home’ key because every note is equally suited to be the tonal center. Because the tuning of intervals is never perfect, tonality becomes somewhat ambiguous. But what you lose in accuracy and groundedness, you gain in flexibility and harmonic mobility. Because the ToneBrick 12 uses only 12 different notes, it has room enough to accommodate each of them twice. This doesn’t add any new notes of course, but it does extend the octave range and makes it easier to play recurring patterns in different keys. This is how the notes are placed in the ToneBrick 12, starting from G:
In scale degrees, it looks like this:
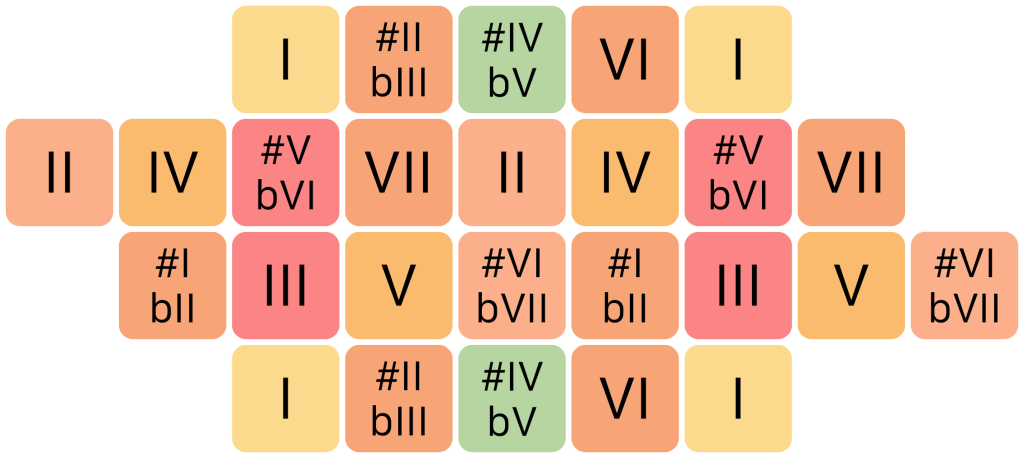
Because the notes are tempered, their ratios are not perfect in this case. However, the intervals between these notes do approximate the most important ratios, with varying accuracy. The colouring of the ToneBrick 12 represents these approximate ratios, with the notes at the corners taken as the tonal center or 1/1 ratio. In an equal tempered system, any of the 12 different notes could be taken as the tonal center. From that point of view, these colours have little meaning, but they still provide a helpful aid to finding your way around the keyboard. This is not unlike the combination of black and white keys on a regular piano: their arrangement only really makes harmonic sense in the key of C, but it still provides important visual and tactile reference in any other key. Below is a map showing the approximate ratios. All of these are somewhat ambiguous, but some more so than others. The keys labeled 5/1 are also the closest approximation of the 1/25 ratio available, but in most musical contexts, the simpler 5/1 ratio clearly overtakes the more remote 1/25. For the keys labeled 9/1 and 5/9, the situation is less clear cut: even though 9/1 is a closer approximation in terms of frequencies, these keys can be used just as convincingly to represent the ratio 5/9. Most ambiguous of all are the #IV / bV keys, where four different harmonic ratios are approximated with nearly equal precision.

The ToneBrick 31
31 tone equal temperament is a very interesting alternative to the much more common 12 tone variety. It has a history that goes back to the sixteenth and seventeenth centuries, long before 12 tone equal temperament became the standard in Western music. It offers a superior approximation of rational intervals while still maintaining all the flexibility of an equal tempered system. Having far more different notes, it is also more complicated, both for the mechanical construction of instruments and in the ease of playing them. In the end, the simpler 12 tone system proved ‘close enough’ for Western music and it seems to me this is probably the main reason it won out. Some note combinations in 31 tone equal temperament can sound quite alien to my ears, but I imagine the same would be true for 12 tone equal temperament if I wouldn’t have been exposed to it all my life.
The most important intervals in music are undoubtedly the first few overtones, the octave, the fifth and the third. When you divide the octave in to twelve equal steps, you get a very good approximation of the rational fifth but a rather poor approximation of the third. When you divide it in to 31 equal steps, you get an excellent approximation of the third while the fifth is only slightly less accurate. You also get clearly recognisable representations of the next few overtones, 7/1, 11/1 and 13/1, whereas these are lost entirely in the 12 tone system.
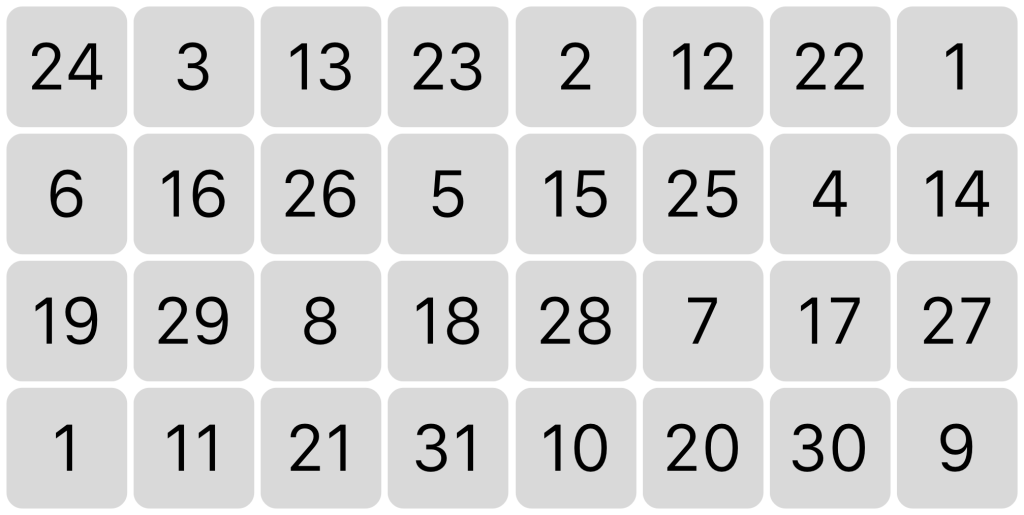
Using the 31 tone system provides many rewards, but finding your way around 31 equally spaced notes without a clear tonal center is not necessarily an easy thing. So it was an interesting challenge to try and make a keyboard that presents these notes in a reasonably intuitive way. I started out by making a 4 by 8 grid, containing just enough keys for a full octave, and arranging the notes so that each step up is always a fifth and each step to the right a major third. This is achieved by jumping 10 notes for every third and 18 notes for the fifths (just as you would jump 4 notes for every third and 7 notes for every fifth in the 12 tone system). Numbering the notes from lowest to highest, the arrangement looks like this:
I then coloured the notes based on the ratios they most closely approximate (see the paragraph ‘keys and colours’ above), taking the first note as root. It now looks like this:
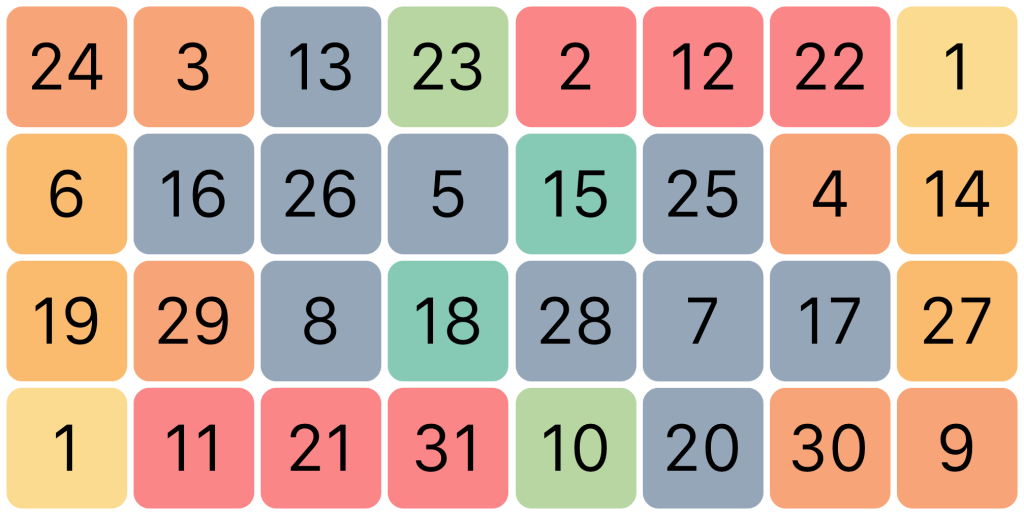
The more familiar ratios (those that are also present in 5-limit just intonation and 12 tone equal temperament) are mainly on the left and right sides of the grid, with the more exotic intervals mainly in the middle. I thought it would be better to have the most common ratios grouped together in the center, so by splitting the grid down the middle and then moving the halves around and lining them up to maintain the harmonic pattern, I obtained this arrangement:

This layout has some interesting properties. First, the broken-up shape, along with the colouring, provides some useful visual clues for navigating the keyboard. Second, the central columns now provide clear and easy access to all the most common diatonic scales. The middle two columns produce the Dorian mode, the most symmetrical and arguably the most universal of all the diatonic scales. Other modes like Ionian (major) and Aeolian (natural minor) are found by substituting one or two notes from the columns directly to the left and right. These scales sound slightly different in 31 tone equal temperament than they do in 12 tone equal temperament, closer to just intonation and with a wonderfully stable and earthy quality to them.
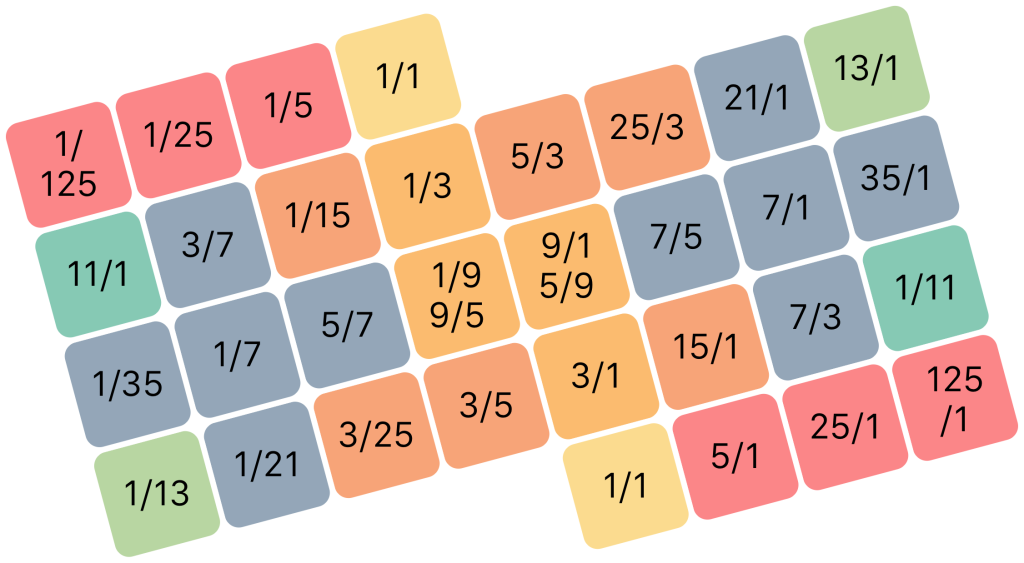
Below are the ratios that best approximate the notes of 31 tone equal temperament to my ears. You can see that the whole tone, or major second, is ambiguous in this case, falling right in between the 9/1 and 5/9 ratios (the same goes for the minor seventh which is a whole tone down rather than up, falling between 1/9 and 9/5). This kind of tuning is also known as a meantone tuning, and that is where the name comes from: the tempered whole tone takes the mean of the two different just intonation whole tones.
For easier reference, below is another illustration showing note names. These are once again only approximate and many different notes share the same name here. There are other ways of naming the notes in 31 tone equal temperament, using more double flats and double sharps, or half-flats and half-sharps, to distinguish each note. I have found these to be more confusing than enlightening, so I have chosen not to use them in this illustration. Like 7-limit just intonation, 31 tone equal temperament simply does not map very well to the standard naming convention. I have found it better to think of these notes as their own thing altogether and identify them by number or colour rather than by note name.

And finally, one more illustration featuring approximate scale degrees instead of note names (to which all the above reservations still apply):

I hope this explains the workings of the different Arithmophone keyboard styles and that it will encourage you to play around with them and experiment freely. If you have any feedback, corrections or suggestions, please let me know!
This page is part of my Arithmophone project.
Arithmophone concept and design by Chiel Zwinkels © 2022
