Arithmophonic design concepts

Introduction

In this article, I will describe the general design concepts behind the Arithmophone keyboards: two dimensional layouts, colour coded keys and octave grouping. The following sections assume a basic understanding of musical notes and intervals, just intonation ratios and temperaments. If you are unfamiliar with these things, everything you need to know can be found in this article. If you are looking for details on a specific Arithmophone keyboard, those can be found in this article.

Two-dimensional keyboards

On a standard piano keyboard, the notes are arranged from low to high (going from left to right). Although the keyboard itself is a 3-dimensional thing, with its raised black keys, this layout is basically one-dimensional: all the notes are arranged along a single line.

The Arithmophone designs on the other hand, use a two-dimensional grid. Arranging the notes in two dimensions instead of one has some interesting advantages, especially for an on-screen keyboard: it can help to make the relationship between different notes more intuitive, make many chords and melodies easier to play and it also makes more efficient use of the available space on the screen.

When we arrange notes in two dimensions, it no longer makes sense to order them simply from lowest to highest, so we need to find some other way of arranging them. We can start by selecting some ratio, for example 3/1, and placing the same ratio between each pair of adjacent notes, like this:

Please note: the ratios shown in the example above and in all the following illustrations, are in their pure, ‘unreduced’ form. The 3/1 ratio is actually a very large interval (an octave plus a fifth). In practice, these ratios will be octave-reduced (ie divided or multiplied by 2 some appropriate number of times) to bring them within a musically useful range. So 3/1 might become 3/2, 1/9 might become 16/9, et cetera. However, this does not change the basic ratio or note it represents, so for clarity and simplicity, unreduced ratios are used throughout this article.

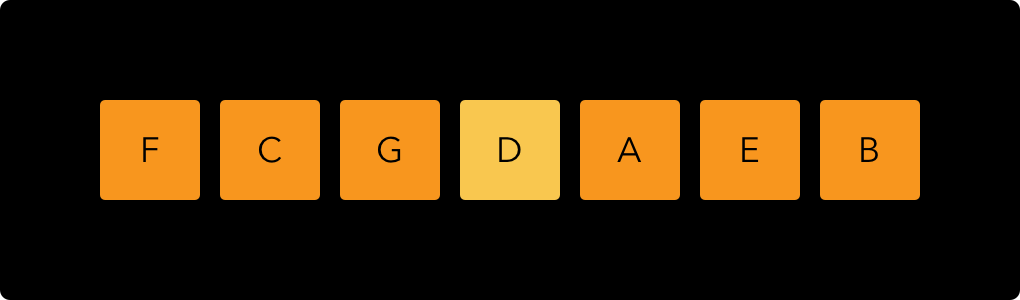
These numbers represent the ratios of the frequencies: if the 1/1 note has a frequency of 100 Hertz, then the 3/1 note is 300 Hertz (3*100), et cetera. Each note has a frequency that is three times as high as the note to the left of it (disregarding octave reduction). In terms of standard note names, taking D as the central note, this example looks as follows:

Once we have this first row of notes, we can chose a different ratio, for example 5/1, for the notes above and below, like such:

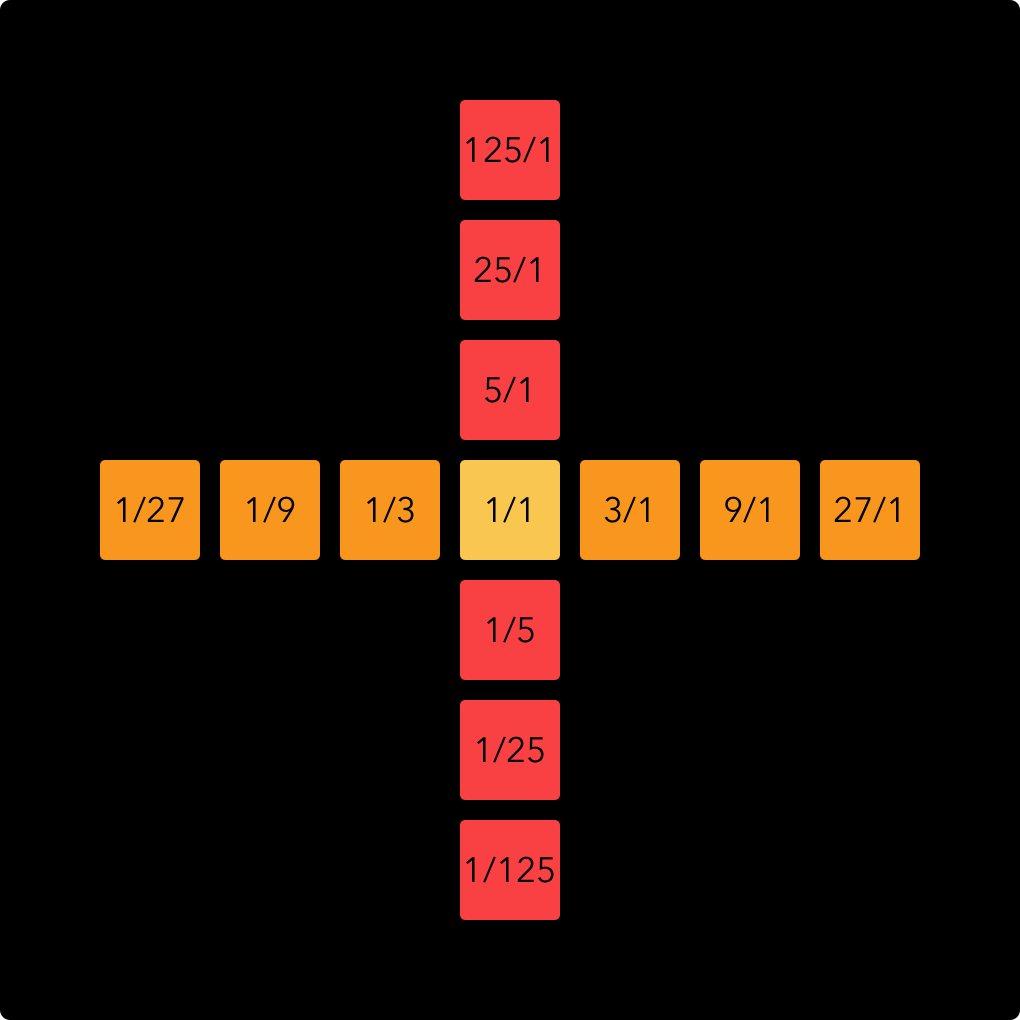
With note names instead of ratios it now looks like this:

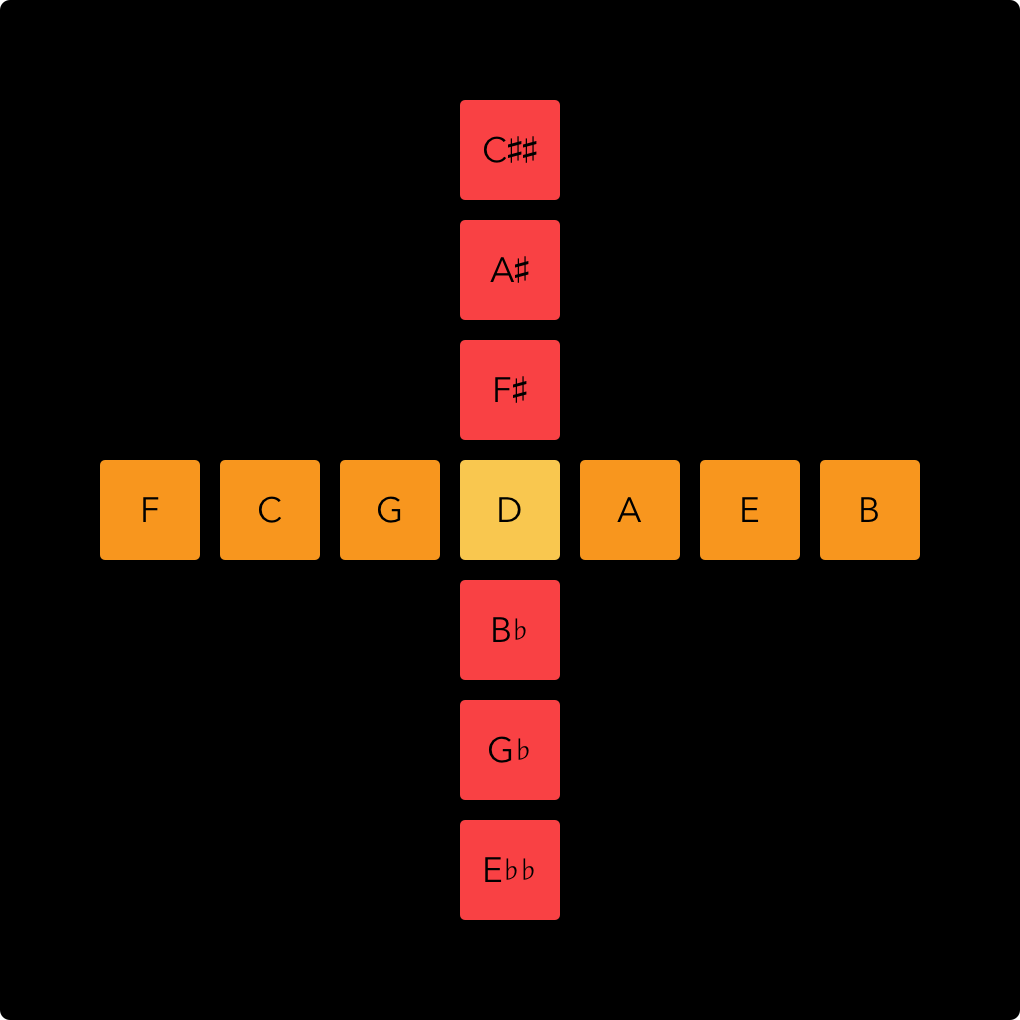
By filling out the other columns we can make a grid like this:

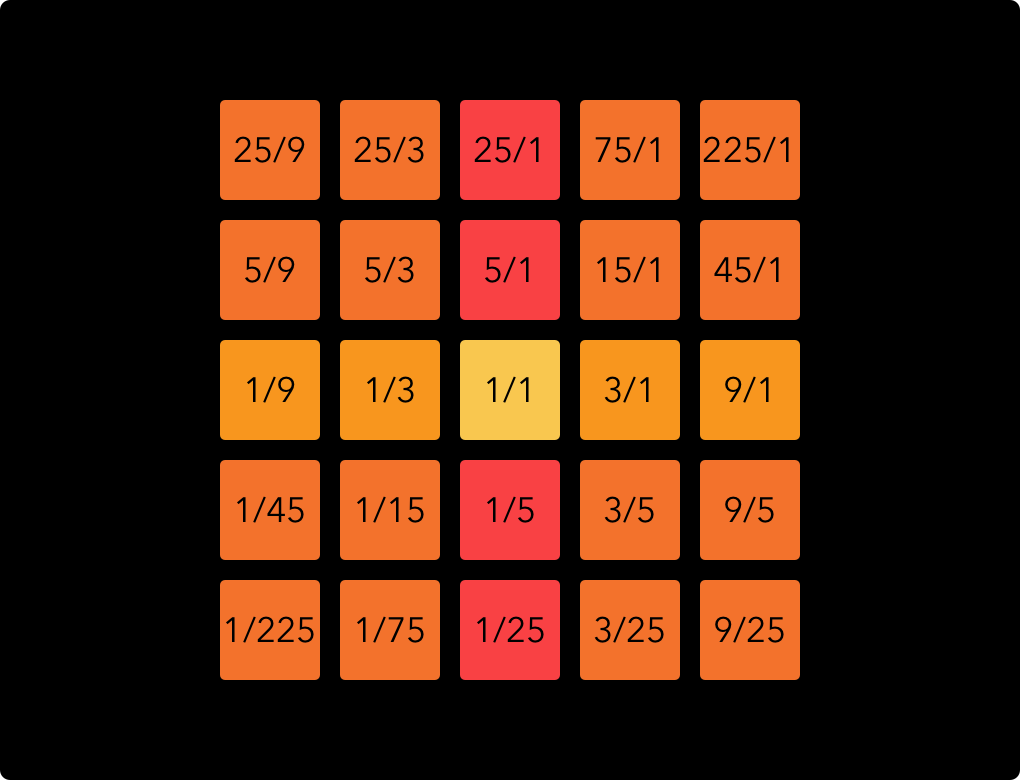
In this way, many musically useful intervals arise. The ratio 3/5 does not appear as a direct over- or undertone of the 1/1 note, but it is present in the column of the 3/1 note and in this way it is strongly (though indirectly) related to the 1/1 as well. 3/5 is in fact the note known as the just minor third, a very common note in almost any kind of music.

With note names instead of ratios, our square looks like this:

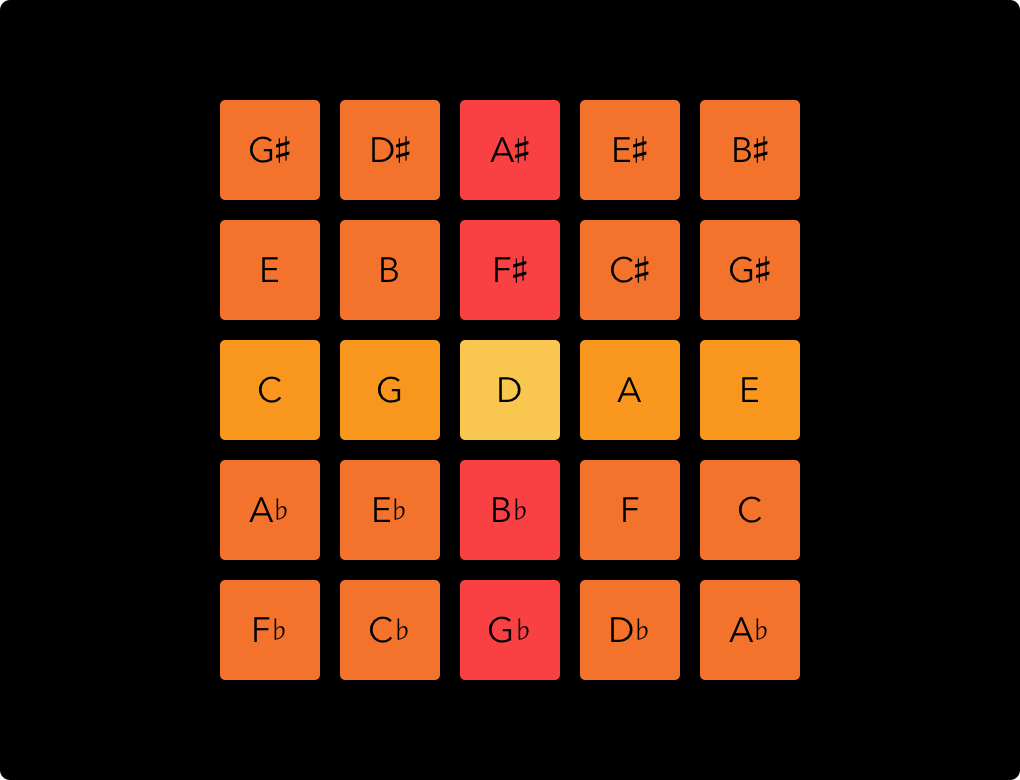
This type of keyboard layout is called isomorphic. That means that wherever you are on the keyboard, moving a certain step always results in the same musical interval. In this example, if you move one step up, you always get a major third, et cetera. Unlike on a piano, once you have learned a certain pattern, chord or melody in one key, you can play it in any other key just as easily.

Harmonic spines

Isomorphic keyboard layouts are well suited for 5-limit just intonation, as described above, and they generally work well for tempered tunings too. On the Arithmophone, variations of these are used for most of the ‘EDO’ keyboard styles. However, for 7-limit just intonation, this type of layout is less suitable. Because each basic ratio (2, 3, 5 and 7) adds its own ‘dimension’ to the selection of notes, you quickly run out of options in a two-dimensional grid. So for the ‘ToneHive’ keyboard, which uses 7-limit just intonation, a different approach was needed.

The ToneHive keyboard is based on what I call ‘harmonic spines’. A harmonic spine is a set of notes that are directly under- and overtonal to a central note. A basic harmonic spine looks like this:

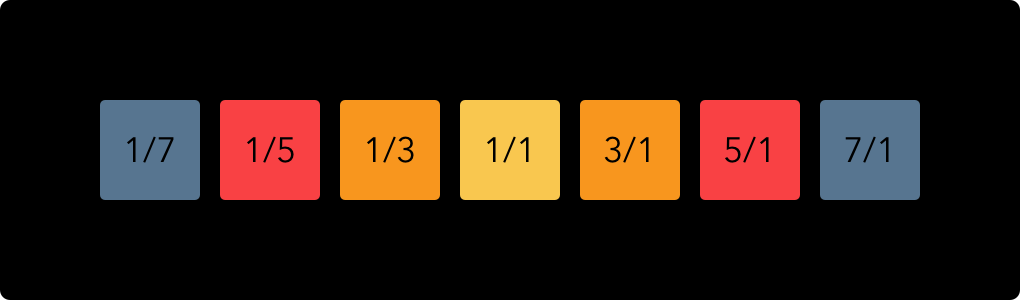
This spine contains all overtones and undertones of the central 1/1 note up to the seventh harmonic. It could in principle be extended as far as desired in both directions, to include the ninth harmonic, the eleventh harmonic et cetera.

Only odd numbers are included, because even numbers don’t introduce any new notes. Those are simply octaves above and below existing notes: 6/1 is an octave above 3/1 and so on. (Strictly speaking, this presupposes the use of an octave-repeating tuning scheme and is not applicable to tuning systems that aren’t octave-repeating, such as the Bohlen-Pierce scale, but those are beyond the scope of this article and the Arithmophone project.)

The 1/1 note forms the center of the keyboard, but a harmonic spine does not have to start on this note, it can be constructed from any note. The example below shows a secondary harmonic spine starting on the 3/1 note.

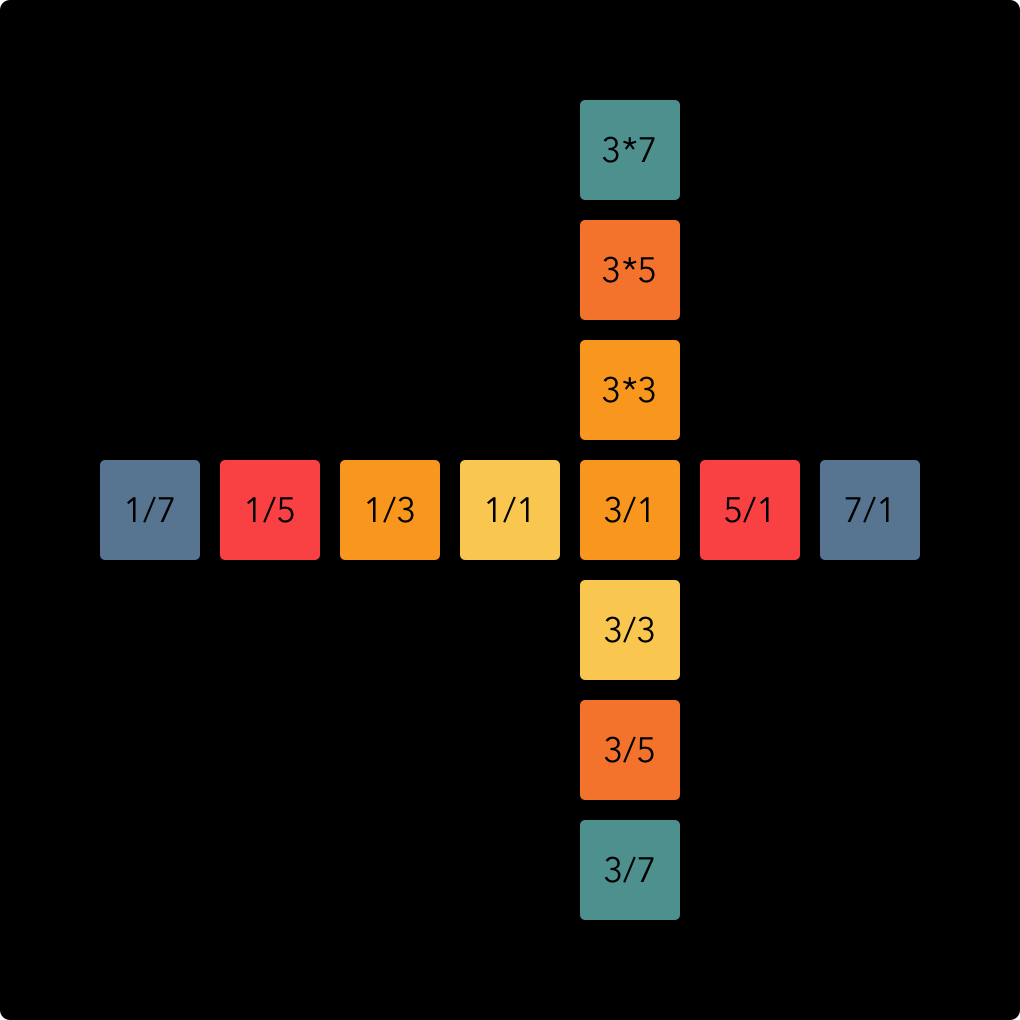
When we extend this principle and use it to make a square of harmonic spines, we obtain many of the most common musical intervals:

However, as a musical keyboard this layout is not very efficient. It generates a lot of duplicates: the same ratios appearing in different places. To remedy this problem, we start by folding the central harmonic spine around the 1/1 ratio like this:

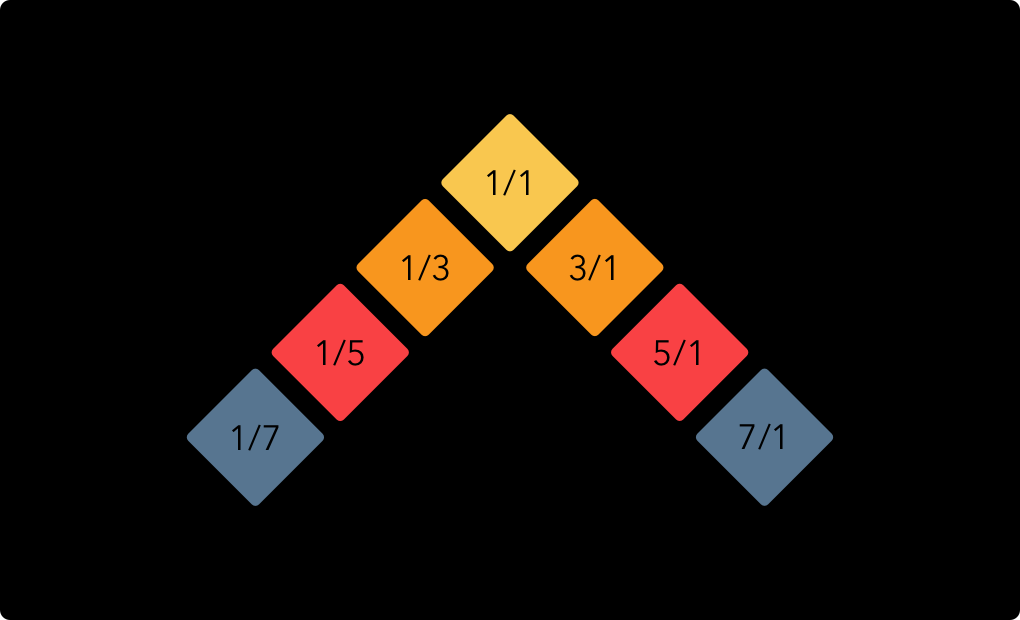
If we start filling in the secondary harmonic spines now, we will see that most of the duplicates land in the same place and therefore become a single key. First we fill in the spines in the inward direction:

And then we can extend it in the outward direction:

Now we have all the same intervals as in the square layout, but we only need slightly more than half the keys. This intertwining of harmonic spines forms the basic harmonic structure of the ToneHive keyboard style.

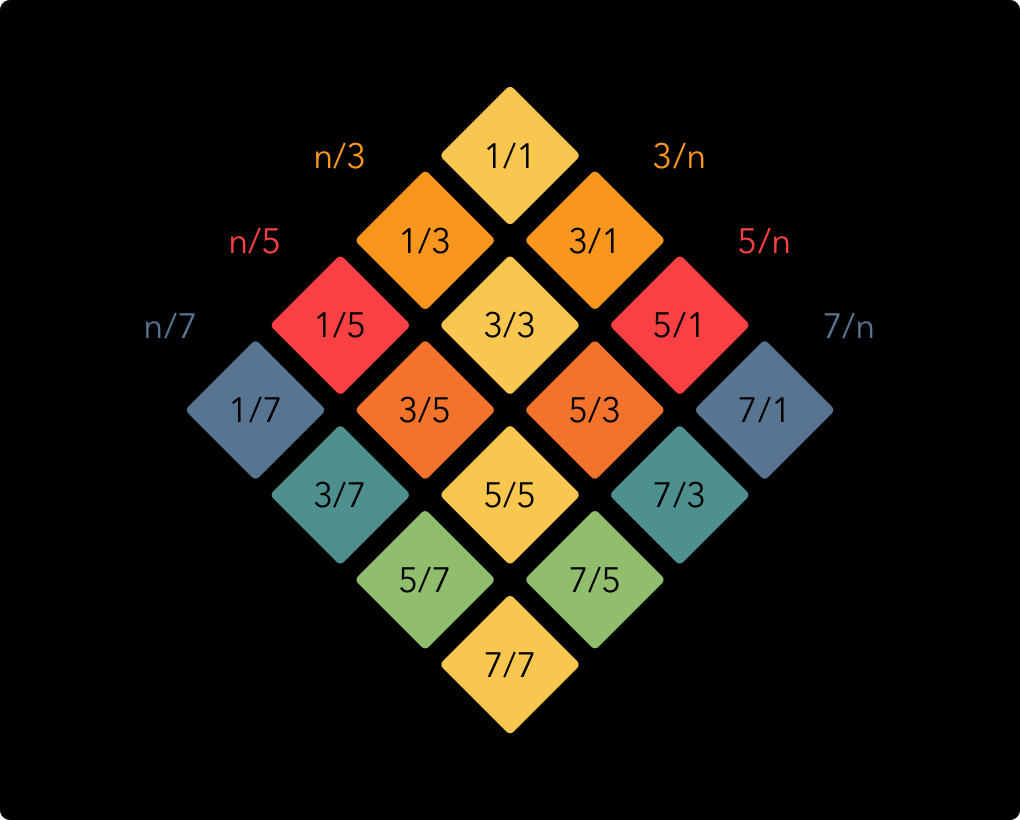
Colour coded keys

On the Arithmophone, the colours of the keys reflect the nature of the interval they form with the central note, which is always marked in light yellow. This provides a useful visual aid for navigating the keyboards. The colour scheme works as follows:

On the ToneHive keyboard, the colours of the keys represent the actual ratios used for the tuning of each note.

The Arithmophone EDO and ChromaKey keyboards use equal temperament tunings, so their notes do not correspond exactly to any ratio. However, they do approximate certain ratios, and this plays an important part in making them musically useful, so I have used approximate ratios for colouring these keyboards. I find these EDO colour codings very useful, not only as a visual aid for navigating the keyboards, but also for understanding the harmonic properties of different EDO’s. However, some caveats are in order:

The colour scheme I used is based on 7-limit ratios. You may prefer to think about a certain EDO in terms of a different limit, like 5 or 11, and this could change many of the note ‘mappings’.
Even within 7-limit ratios, I could have chosen different ratios. For example, 9/1 and 5/9 are pretty close together (they reduce to 9/8 and 10/9) and an EDO step may well fall in between them. In such cases, I have usually preferred the simplest ratio, even if that has a somewhat larger tuning error, and tried to map the entire EDO to a coherent set of ratios. However, this is often a highly subjective process.
You could argue that rational approximation doesn’t represent the essence of EDO tunings. I would mostly disagree, but a pretty convincing case could be made.
EDO tunings don’t have actual roots, so all notes are equal. This means that singling out any one note could be considered misleading. This is definitely a valid criticism, but it also applies to a regular piano keyboard, yet its ‘unequal’ arrangement of 7 white and 5 black keys has proved to be quite an enduring success.

Octave grouping

Unlike on most instruments, the physical distance between notes on the Arithmophone keyboards generally does not correspond to their distance in pitch, but to their harmonic distance. Because the shortest possible harmonic distance between to notes (that aren’t identical) is the octave, it made sense to me to group together different octaves of the same notes. This also solves a big problem inherent in using scales with much more than 12 notes per octave, namely that their layout can becomes very unwieldy. Using octave grouping allows for a clean and relatively simple keyboard design that still spans a range of several octaves. I have designed each of the Arithmophone keyboards in such a way that it covers at least a full three octave range, using double or triple octave keys wherever this seemed like the most efficient solution. An example of how this works can be seen in the illustration below, with ratios in the top row and 12-EDO steps in the bottom row.

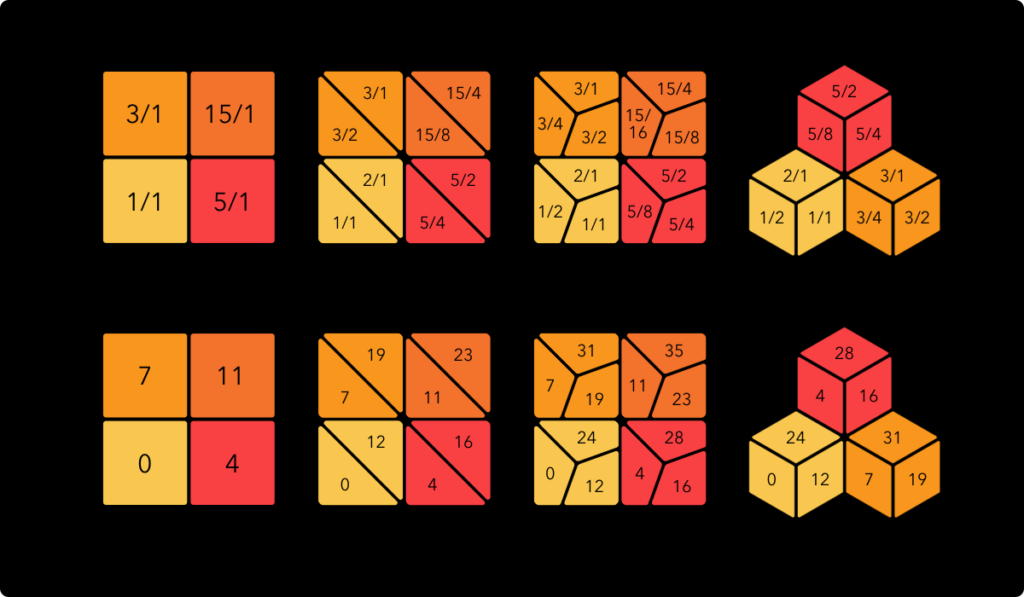
To learn more about the design of the individual Arithmophone keyboards, continue reading with this article.