Introduction
In this article, I will describe each of the Arithmophone keyboard designs in some detail. I also discuss ‘quasi 3-5 grids’ and the way I used rational approximations for the colours of the EDO keyboards.
The following sections assume a basic understanding of musical notes and intervals, just intonation ratios and temperaments. If you are unfamiliar with these things, everything you need to know can be found in this article. For a more general discussion of the design concepts behind the Arithmophone keyboards, please read this article.
7-limit just intonation
The ToneHive keyboard uses 7-limit just intonation tuning. This produces many intervals that are very different from standard (12 tone equal temperament) tuning, which mainly provides useable approximations for 5-limit intervals. Expanding this limit to 7 introduces a whole new class of notes, that are not really represented in standard music theory, although they do appear frequently in many kinds of music, like Blues and Jazz, at least on instruments with flexible tuning like slide guitars and saxophones (and of course in singing). These notes are often referred to as ‘blue notes’, a fact I have used as inspiration for the colour scheme of the Arithmophone.
Aside from producing original intervals, septimal ratios can also double as pretty good approximations of 5-limit intervals. This is because, after octave reduction, the 7/1 ratio is very close to 225/1. This is known as the ‘septimal comma’. The difference between these two intervals is only 225/224, or about 7.7 cents (a cent is 1/100th of a standard semitone). This is close enough that our ears can easily perceive these notes as functionally equivalent; considering the fact that our ears routinely accept the 13.7 cents tuning error that 12 tone Equal Temperament causes for the major third, it is actually quite accurate. This means that every 7-limit ratio has a 5-limit ‘twin’, and vice versa. For example, if we start on 9/1 and want to add a major third (5/1 ratio) above, we would normally use 45/1 (because 9*5 is 45). This ratio is not present on the Arithmophone ToneHive, but it’s ‘twin’ 7/5 is and produces a perfectly useable major third in combination with 9/1.
The ToneHive keyboard
The layout of the ToneHive keyboard is based on the idea of harmonic spines. However, in order to create an interesting and coherent selection of notes, I have taken some liberties with this basic structure. Harmonic spines are used up to the 7th harmonic, but multiples like 9 or 15 don’t get their own spine. Instead, I have created a ring of notes around each of the intervals 7/1 and 1/7, filled out with a few remaining 5-limit notes that don’t appear in the basic spines but are still important in relation to the other notes that are present. In total, there are 41 different notes on the ToneHive keyboard. In basic ratios, it looks like this:
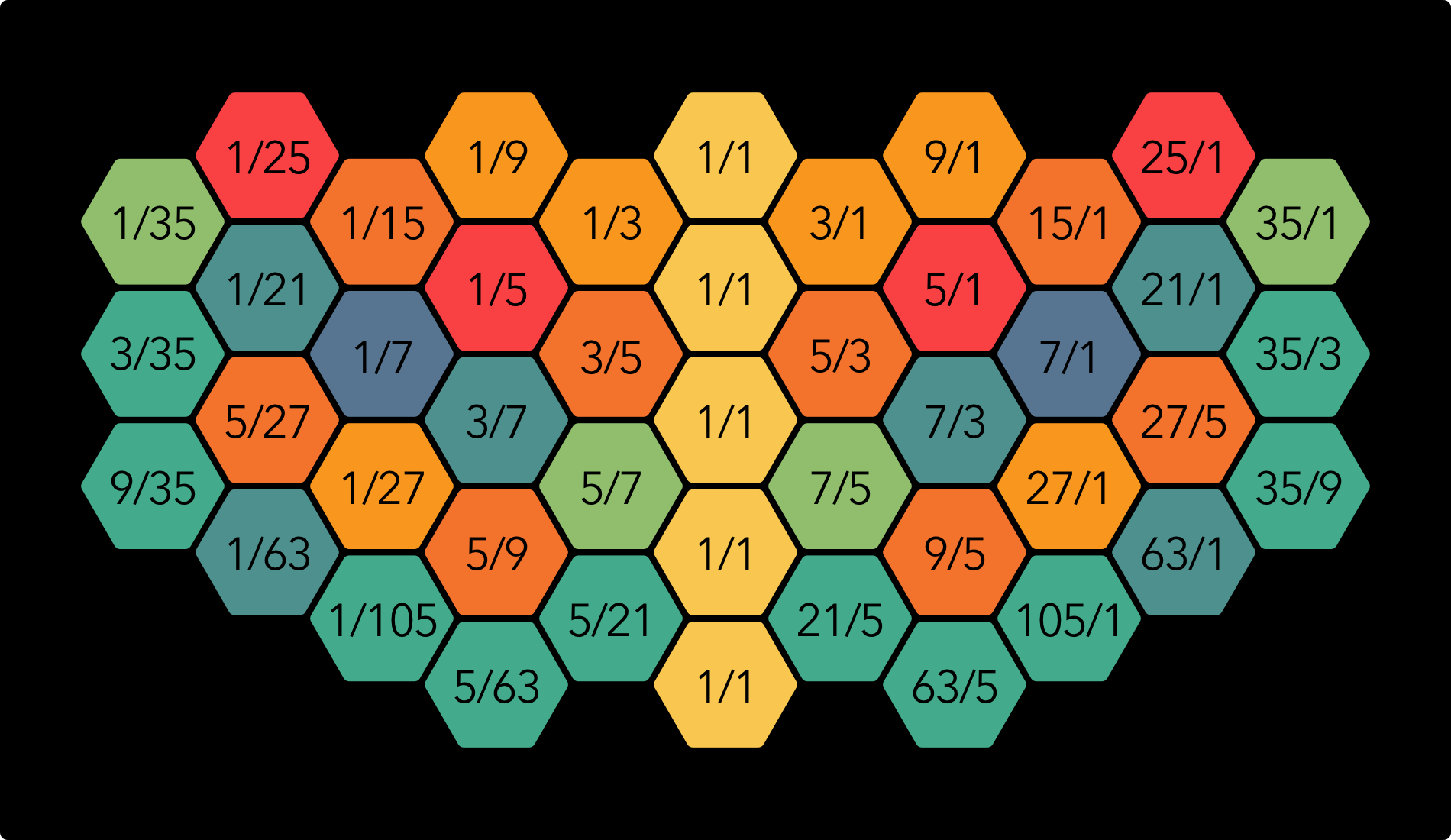
This makes for three different areas: the notes in yellow, orange and red are all 5-limit intervals, centered directly around the 1/1. The blue and green notes on the left are centred around 1/7 and form their own coherent subset of 5-limit intervals. The same thing applies to the blue and green notes on the right, except that those are centred around 7/1. These three main areas are connected in two different ways: by a direct leap of 7/1 or 1/7, but also by the close relations created by the 225/224 exchange.
The illustration above contains a lot of accurate information, but it is probably not very easy to digest. Below, I have included an illustration with note names instead of ratios, using the note ‘D’ for the 1/1 ratio (why D? See here), which is a lot easier to read. However, in 7-limit just intonation the mapping of ratios to note names is quite tricky. I have chosen to represent the 7/1 ratio as B# (starting from D). This implies thinking of the seventh harmonic functionally as a raised sixth rather than a flat seventh, which is somewhat unconventional, but has the advantage that it makes every combination of note name and colour unique on the Arithmophone ToneHive. I also found it quite helpful in relating this interval to it’s 5-limit ‘twin’ 225/1 and distinguishing it from it’s 5-limit ‘cousins’, the 1/9 and 9/5 flat sevenths.

The Quasi 3-5 grid
There is another way of representing the notes on the ToneHive that I have found helpful, and that is in a ‘quasi 3-5 grid’. A regular 3-5 grid uses the horizontal axis for 3/1 note relations and the vertical axis for 5/1 note relations. This is very effective for 5-limit intervals, but it lacks an axis for septimal ratios. However, because of the closeness of septimal ratios to 5-limit ratios by the 225/224 comma, we can substitute these notes on the grid in the place of their ‘twins’. So 7/5 takes the place of 45/1, 25/1 takes the place of 7/9, et cetera.
Of course this only works as long as we don’t use both ‘twins’ in the same keyboard, but the ToneHive never does that. In this way, we can create a ‘map’ of the notes on the keyboard, highlighting their (quasi) 5-limit relations, like so:

This shows very clearly how the 7-limit notes can double as extensions of the central 5-limit notes (and vice versa).
There are other ‘harmonic wormholes’ to be found in the ToneHive keyboard, too. For example, the jump from 35/1 to 3/35 (or 35/32 to 48/35, after octave reduction) is only 5.4 cents removed from a just major third, even closer than the 225/224 interchange. This means that with some careful planning, we can modulate ‘all the way around’ the ToneHive in different ways, giving it considerable harmonic flexibility. In the following illustration, I have connected four copies of the ToneHive’s ‘quasi 3-5 grid’ together to further illustrate these harmonic connections (I have put in note names instead of ratios to make it a bit more legible).
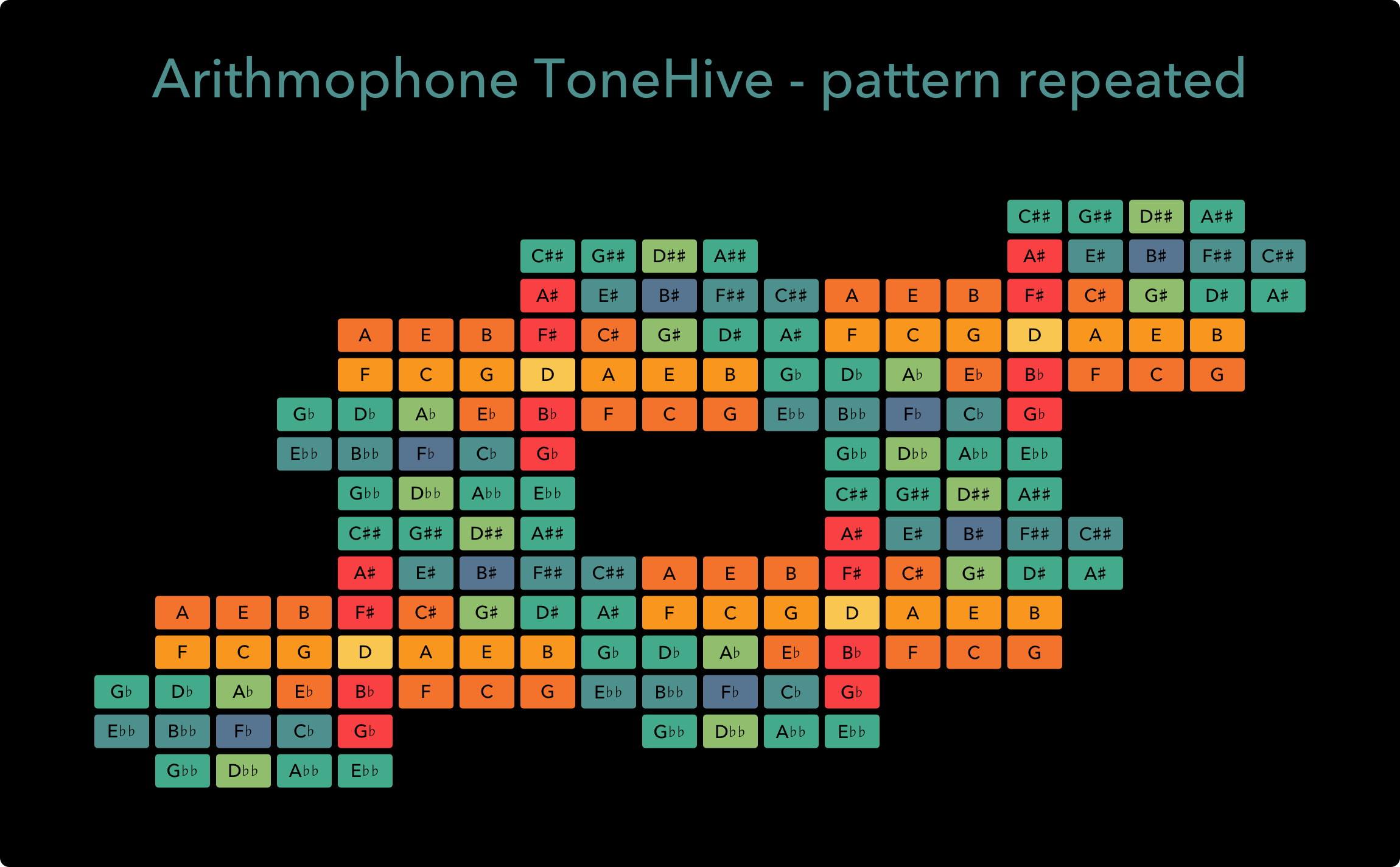
In this diagram, each horizontal step represents a reasonably accurate musical fifth, while each vertical step represents a decent musical third. The hole in the middle of the diagram makes it clear that the note selection of the ToneHive could also be seen as part of a larger temperament. We could complete this by adding 12 more ratios, for example those shown below:
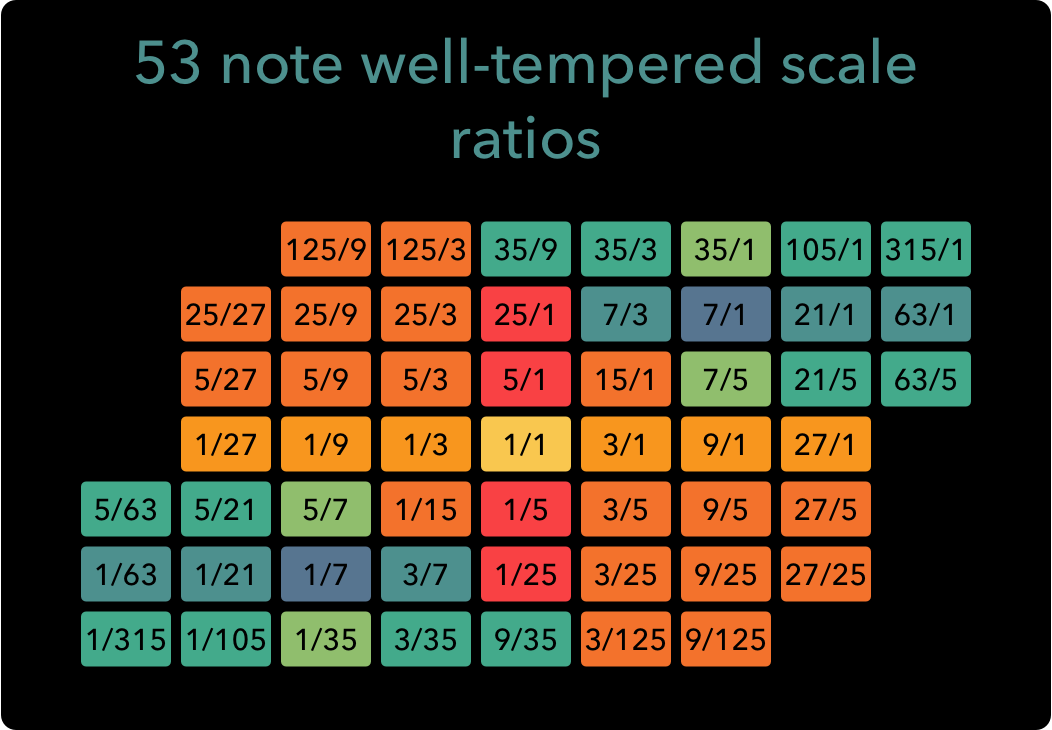
This creates a 53 note ‘well temperament’ with some very interesting properties. It contains many exact 7-limit intervals, yet it also functions as a complete 5-limit temperament with tuning errors that never exceed 7.7 cents. Although this is a bit beyond the possibilities actually present on the ToneHive, I believe it could be of interest as a compositional system. It does require 53 notes per octave, at which point one could also consider just using 53 tone Equal Temperament. In 53 EDO, both the thirds and the fifths are nearly perfectly tuned, so from a 5-limit perspective, this would certainly be preferable. However, the seventh harmonic in 53 EDO is off by about 4.8 cents, so in some contexts, the 53 note “well temperament” presented above might actually be more advantageous.
Equal temperaments
The Arithmophone provides keyboards for 6 different equal temperament or EDO (Equal Divisions of the Octave) tunings. 12 EDO, also known as 12 tone Equal Temperament, is by far the most familiar of these; it is the predominant tuning system of Western music, whether classical, jazz, pop, electronic or what-have-you. Historically, it came to prominence as a practical alternative to just intonation tuning, because it offered a good combination of reasonable approximations of 5-limit intervals with a manageable number of different notes.
Long before 12 EDO became the standard practice, there were already many musical instruments that had 12 notes per octave (organs, harpsichords et cetera). These were originally tuned in other ways, based just intonation intervals. However, having only 12 different notes available imposes a lot of limitations in just intonation. If we take the note D as the 1/1 ratio, a basic first step would be to tune G to 1/3 and A to 3/1. Once these notes are set though, complications arise almost immediately. For example, how should we tune our E? If we want to be able to play a well-tuned A major triad, it should be tuned to 9/1 so it will form a proper fifth with our A. But if we want to be able to play an E minor triad, it should be tuned to 5/9 so it will form a proper minor third with our G. We can have a perfect A major chord or a perfect E minor chord, but not both. And this is only the beginning of the complexities that arise. In order to optimize the keyboard for one key, some other keys need to be seriously compromised. This is where tempered tunings come in: they spread out the tuning errors across the available notes, so that more intervals become useable. The trade-off is that less, if any, intervals remain perfectly tuned.
In retrospect an equal temperament, which spaces all notes equally so that all keys are equally in/out of tune, seems like the obvious solution for this problem. However, it took a long time before 12 EDO was universally accepted. This has to do with the fact that the tuning of musical thirds is quite seriously compromised in 12 EDO. The major third (5/1 ratio) is off by 13.7 cents, while the minor third (3/5 ratio) is off by 15.6 cents. These are quite large tuning errors, giving the thirds a kind of restless, pulsating quality that we have grown accustomed to these days, but that people objected to fervently in a time when rational tuning was still the norm. Many different approaches were tried to find a better compromise. Some of these focused on tuning the 12 notes in such a way that most of the intervals in most keys sounded more palatable than in 12 EDO, at the expense of leaving a few keys worse off. Others tried using a larger numbers of different notes, to allow for more accurate approximations of just intonation. There were keyboard instruments with 19 keys (using split black keys and extra keys between B and C and between E and F) and tuning systems with as many as 31 notes per octave were regularly used for the intonation of flexible pitch instruments like the violin.
In the end, the convenience and cross-instrument compatibility of 12 EDO won out in the Western world, but it’s interesting to think how easily this could have gone another way. Perhaps if the average ears would have been just a little bit more sensitive to the intonation of musical thirds, the Western world would have settled on 19 EDO a few centuries ago. Or conversely, if people would have been just a bit less sensitive to intonation, it might have settled on 7 EDO, which certainly is a lot more convenient than 12 EDO, eliminating the need for black keys, sharps and flats all together.
In designing electronic instruments, we no longer need to worry about the added cost and complexity of adding more strings/reeds/organ pipes, and using a larger number of notes per octave becomes a compelling option once again. Even 53 EDO, which was described in theory as early as the first century BC (!), now becomes reasonably practical. The Arithmophone showcases several of the ‘alternate reality’ EDO systems. The specific EDO numbers (7, 12, 19, 22, 31 and 53) were selected based on their performance in the approximation of just intonation intervals. You might think that, the larger the number of EDO steps, the better the approximation, but this is not really the case. For example, 15 EDO is just as bad as 12 EDO at thirds and much worse at fifths, while 37 EDO is pretty good at thirds but much worse than 12 EDO at fifths. There are some ‘goldilocks’ numbers to be found though, that perform extremely well relative to their number of steps: they offer a good compromise between complexity and accuracy. Some of these are the EDO numbers that are featured on the Arithmophone.
Rational approximation colours on the Arithmophone EDO keyboards
The colours of the keys on the Arithmophone keyboards were chosen based on their approximation of 7-limit just intonation intervals. I developed this colour scheme for the ToneHive just intonation keyboard, but I decided to apply it to the EDO keyboards as well. It emphasizes the conncetions between EDO notes and rational intervals, and I found it very helpful for finding my way around new Keyboard layouts / EDO systems. It should be noted that this ‘rational approximation colouring’ is a tricky process that includes a number of somewhat arbitrary decisions. EDO notes do not inherently correspond directly to any particular ratio. Instead they can fulfil the function of several different ratios. To make this clear, let’s look at the familiar 12 EDO. Below is a table of each of the notes of 12 EDO with some of the most obvious rational intervals they may represent, as well as the tuning errors that arise in these approximations:
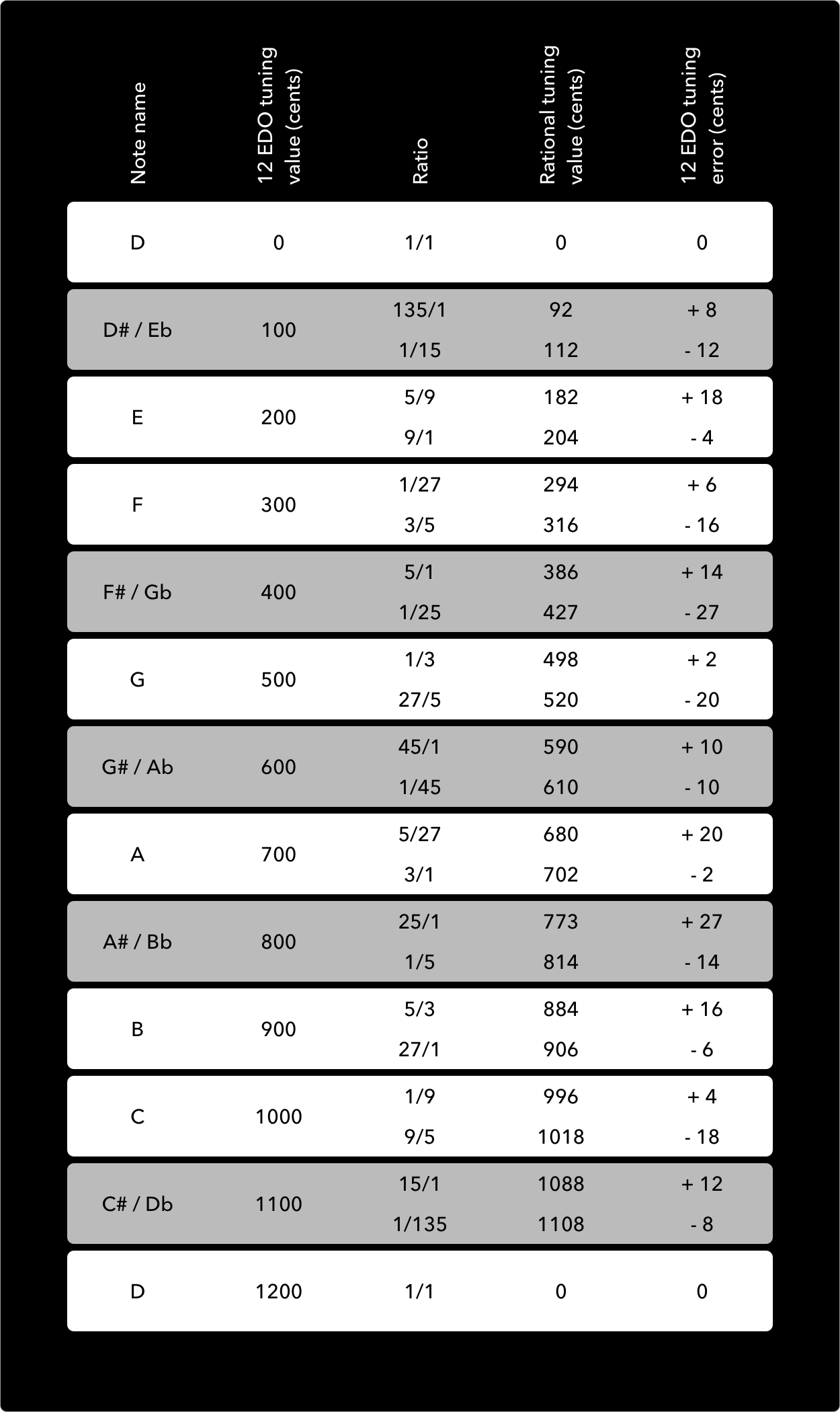
I called these ratios obvious options, but that does not mean that they are the closest possible rational approximations for the notes of 12 EDO. For example, the F# of 400 cents is actually quite close to the 81/1 ratio of 408 cents, and an even better approximation would be 17/27, which is 399 cents. The reason that the 5/1 ratio of 386 cents is still a more obvious choice, is that the 5/1 ratio is one of the most fundamental intervals in music, the major third. When interpreting the notes of an EDO, I feel that a decent approximation of a very basic ratio should always win out over an excellent approximation of a much more exotic ratio. But there are no clear lines here, and while the choice between 17/27 and 5/1 may be obvious, many other choices, such as the one between 45/1 and 7/5, certainly aren’t.
To better understand how all these ‘obvious’ ratios are related to each other, it is helpful to visualize them in a 3-5 grid, like so:

This shows that these notes form a coherent ‘block’ of connected ratios, all related to each other through 3/1 and 5/1 intervals.
Now, when we consider 12 EDO in isolation, it makes sense to stick with 5-limit intervals like in the examples above. This is because 12 EDO has only a small number of different notes and it doesn’t approximate higher limit ratios very well. One of the interesting things about larger EDOs is that they expand the number of ‘obvious’ ratios to include higher limit notes. For example, EDO 31 provides an excellent approximation of the 7/1 ratio. But even in 12 EDO, the realm of 7-limit notes can sometimes ‘shine through’, especially on sharp fourth/flat fifth ‘blue notes’. These can be represented as 45/1 (or 1/45), but also as 7/5 (or 5/7). The actual tuning of these notes in 12 EDO is a bit closer to 45/1, but 7/5 is arguably the simpler ratio, especially if you take octave reduction in to account. From this perspective, 45/1 comes out as 45/32 = (3*3*5)/(2*2*2*2*2), which is certainly a lot more ‘harmonic jumps’ than just plain 7/5.
If we replace the 3-5 grid from the previous illustrations with a ‘quasi 3-5 grid’, using 7/5 and 5/7 as the ‘turning points’, we get this picture:

I have chosen to use this colouring for the 12 Arithmophone EDO keyboard, rather than the 5-limit version. Even if it’s debatable whether or not 7/5 is a more essential ratio than 45/1 (I do tend to think so), this version provides a clearer connection to the ToneHive and the other EDO keyboards and the extra colour is quite helpful in navigating the keyboard.
Of course, the grid pictured above still shows many more ratios than there are notes in 12 EDO. In order to get to an actual colour scheme for the keyboard, we need to trim it down. This too involves some pretty subjective decisions. I ended up choosing this group of ratios because I felt that they represented the best combination of accuracy, simplicity and coherence.
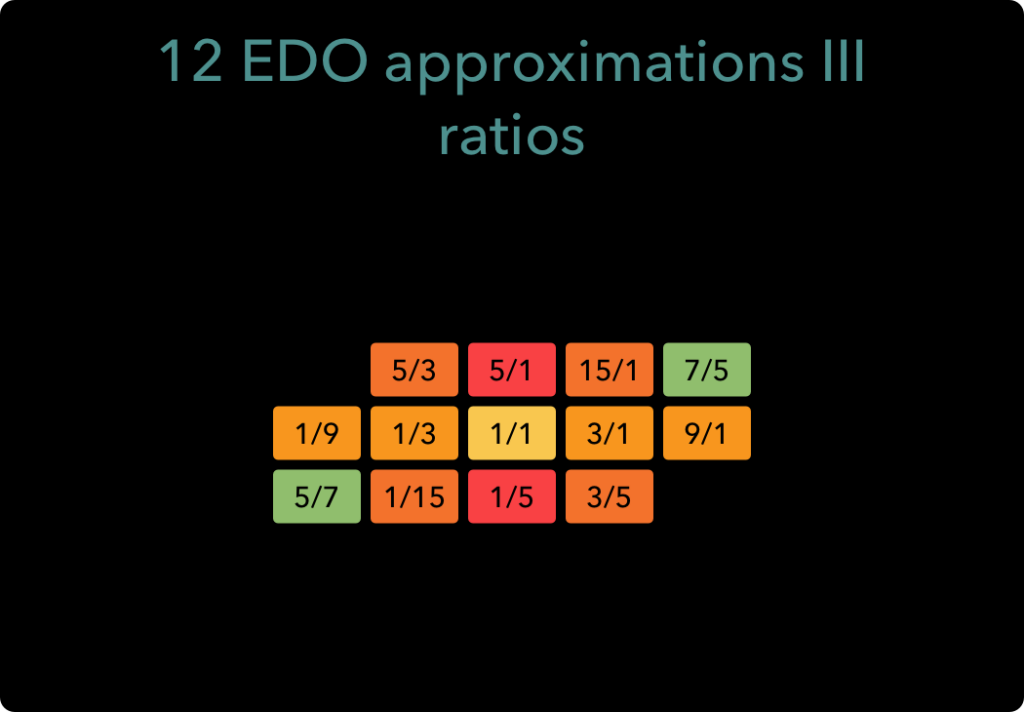
This is still 13 ratios, so one too many for 12 EDO, but the 7/5 and 5/7 ratios map to the same note (G#/Ab) and they both have the same colour, so this doesn’t affect our colour scheme. Using note names instead of ratios, the final colour coding looks like this:
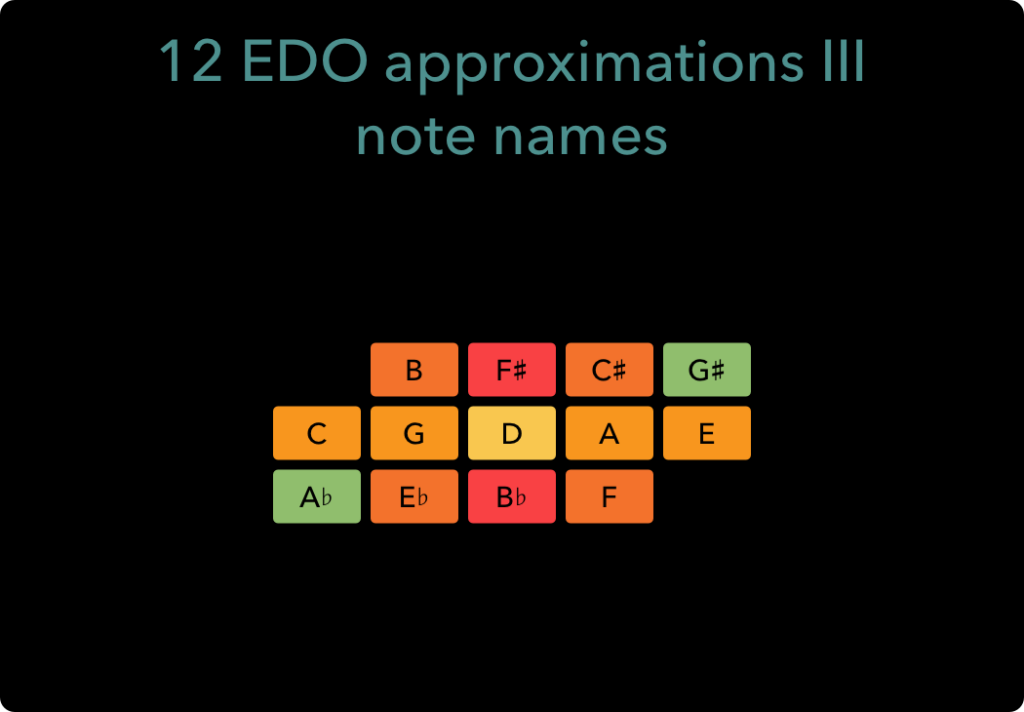
I have used a similar process to determine the colour scheme for each of the EDO keyboards. A chart of their particular ‘quasi 3-5 grids’ is included for reference at the end of this article.
A final few remarks about these colour schemes before we can get on to the actual keyboard designs:
- The rational approximations I used are based on 7-limit intervals. You may prefer to think about a certain EDO in terms of a different limit, like 11 or 13, and this could change many of the note ‘mappings’.
- You could argue that rational approximation doesn’t represent the essence of EDO tunings. I would mostly disagree, but a pretty convincing case could be made.
- EDO tunings don’t have actual roots, so all notes are essentially equal. This means that singling out any one note could be considered misleading. This is certainly a valid criticism, but it also applies to a regular piano keyboard, yet its ‘unequal’ arrangement of 7 white and 5 black keys has proved to be quite an enduring success.
In the end, these colour schemes are only paint jobs, which hopefully are helpful and pleasing to the eye, but can never capture all the intricacies of the relationship between equal temperaments and rational intervals.
7 tone Equal temperament: the ‘EDO 7’ keyboard
In this temperament, each letter of the diatonic scale gets just one note: there are no sharps or flats. This also means there is no major or minor, there are only ‘plain’ thirds, somewhere in between these. This is very limiting, but can sound quite interesting too. For ears tuned to 12 EDO, chords in 7 EDO can take on major or minor ‘flavours’, depending on their position in a progression. This temperament is also quite well suited to pentatonic music. On the ‘EDO 7’ keyboard, the notes are arranged like this:

Horizontally, the notes ascend from left to right by 4 EDO steps, which form a musical fifth. Diagonally, they move by 2 steps, which form a musical third. The notes in 7 EDO are not very close to the most basic ratios, but our ears (well, mine at least) still try to interpret them in such a way. This can create some interesting shifts, where the same scale can sound major-like, minor-like or wholetone-like, depending on context. I used what seemed to me the most reasonable rational approximation for the colours of the keyboard. With ratios filled in instead of EDO step numbers, the keyboard map looks like this:

And with note names instead of ratios, taking a D as the center, the map looks like this:

12 tone Equal temperament: the ‘EDO 12’ and ‘ChromaKey’ keyboard
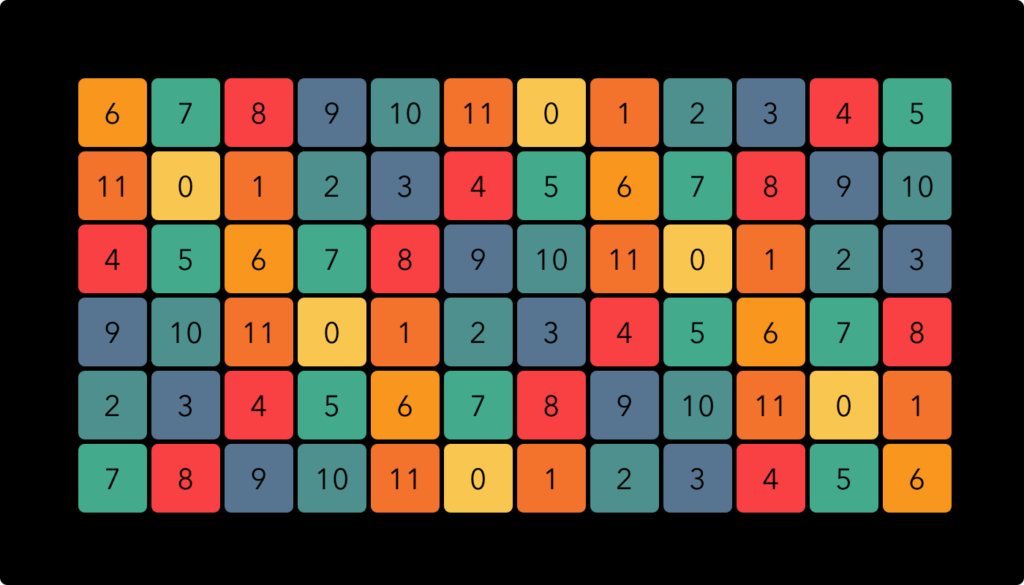
This temperament is the familiar standard of Western music. It is used in the construction and tuning of guitars, pianos and many other ‘fixed pitch’ instruments. It offers a great balance between simplicity (not too many different notes) and decent approximations of the most important harmonics. On the ‘EDO 12’ keyboard, the notes are arranged like this:
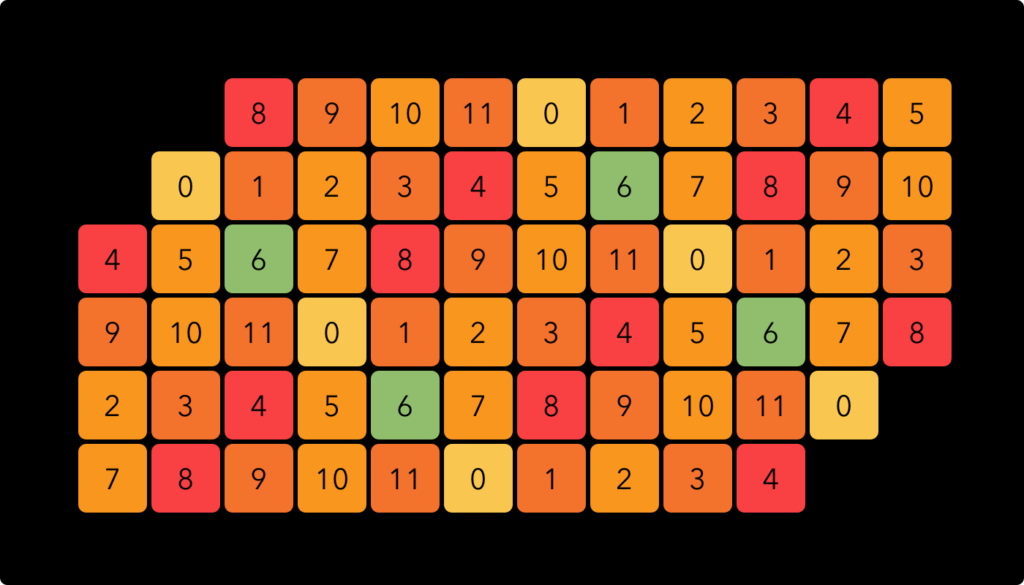
Horizontally, the notes are in ascending order from left to right. Vertically, each row up is a jump of 7 semitones, which form a musical fifth. This layout is similar to the way the string are tuned on a cello or a violin, except in this case you have 6 horizontal “strings”. This does mean that most notes appear more than once, as they would on a cello or a violin. This is not the most economic way to arrange a two-dimensional keyboard, but the added redundancy does improve the ease of playing and in the case of 12 EDO, this seemed like a good trade-off.
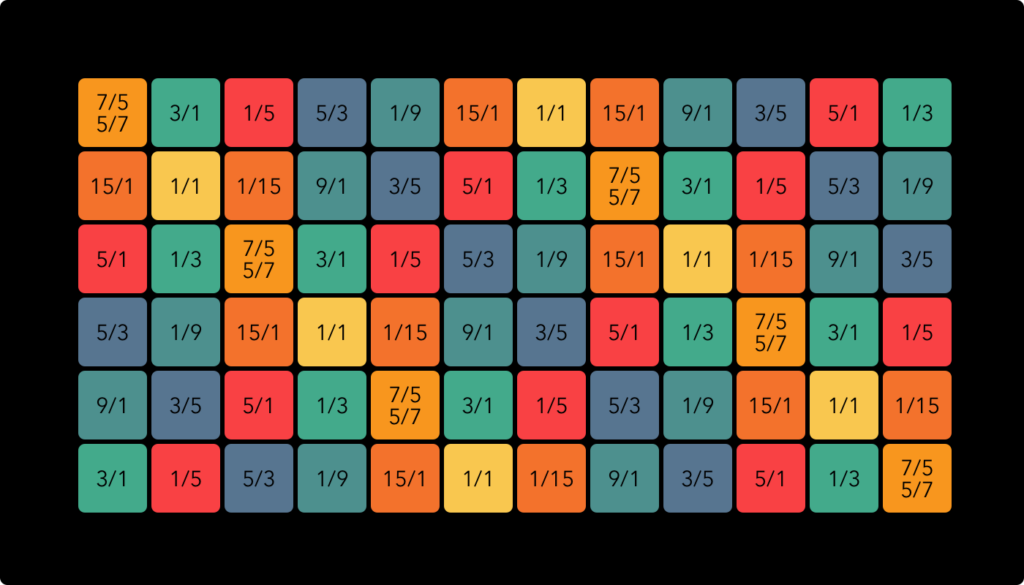
The approximate ratios used for the colour scheme are as follows:

The 7/5 ratios I used may not be the most obvious choice. The augmented fourth / diminished fifth in 12 EDO is usually interpreted as a 45/1 or 1/45 ratio (commonly notated with octave reduction as 45/32 or 64/45). This makes a lot of sense: these ratios are actually a little closer to the EDO value than the 7/5 and 5/7 ratios and this keeps the whole system within 5-limit intervals. However, I do feel that this note is the one place where 7-limit harmony ‘shines through’ in 12 EDO and I wanted to represent that. Also, adding an extra colour made the whole keyboard much easier to navigate visually.
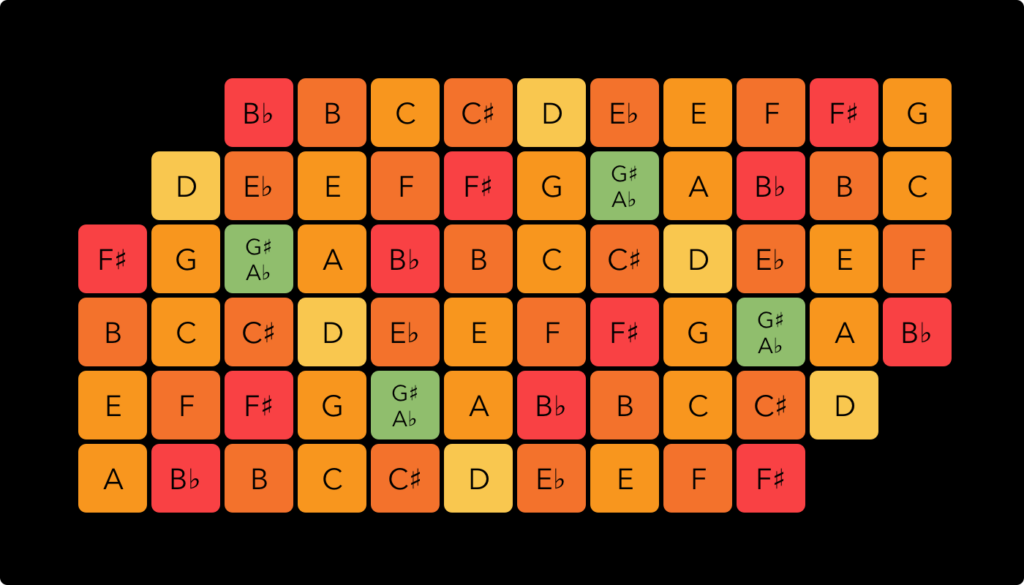
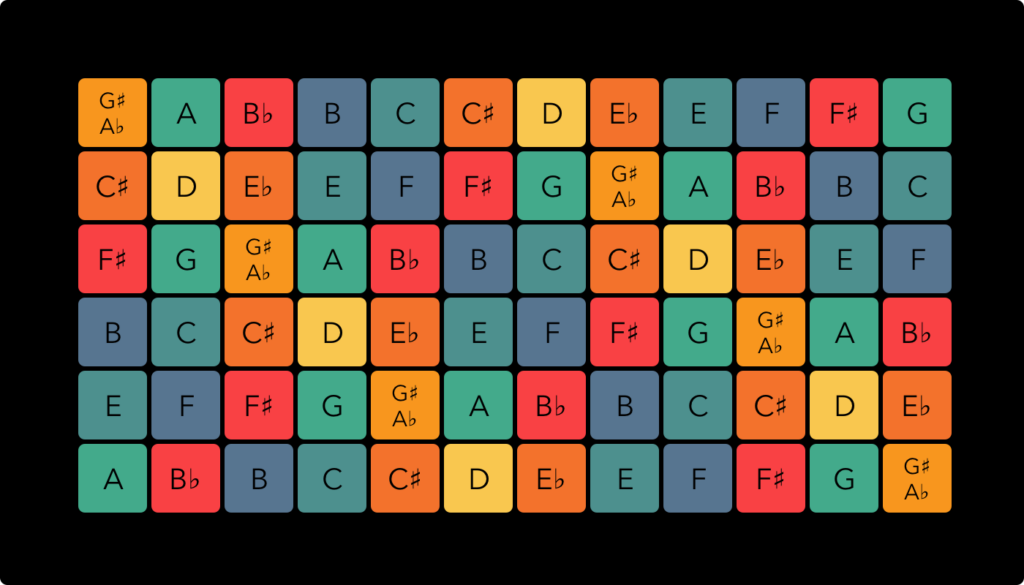
With note names instead of ratios, taking a D as the center, the map looks like this:
The ‘ChromaKey’ Midi Arithmophone uses a variation on this keyboard layout. It has the same 12 EDO tuning scheme and is practically identical, except that it fills out the gaps on the upper left and lower right (adding some more duplicate notes) and that it uses a different colour scheme. This colour scheme is a kind of ‘double rainbow based on the circle of fifths:

This colour scheme is not very informative from a ‘rational approximation’ viewpoint, but it makes better use of the available colours and I like the way it looks, so I decided to go with this variant for the Midi version.
The EDO steps and note name diagrams for the ChromaKey are nearly the same as those for the EDO 12, but for the sake of completeness, I have included them below:
19 tone Equal Temperament: the ‘EDO 19’ Keyboard
Historically, this temperament was a strong competitor for the now dominant 12 EDO, and with good reason. It provides a much closer approximation of the very important musical thirds (5/4 and 6/5 ratios) than 12 EDO. The trade-offs are that the musical fourths and fifths (4/3 and 3/2 ratios) are a bit less in tune, and of course that there is a larger number of different notes to deal with. However, I think it has a lovely open and sweet sounding quality to it. On the ‘EDO 19’ keyboard, the notes are arranged like this:
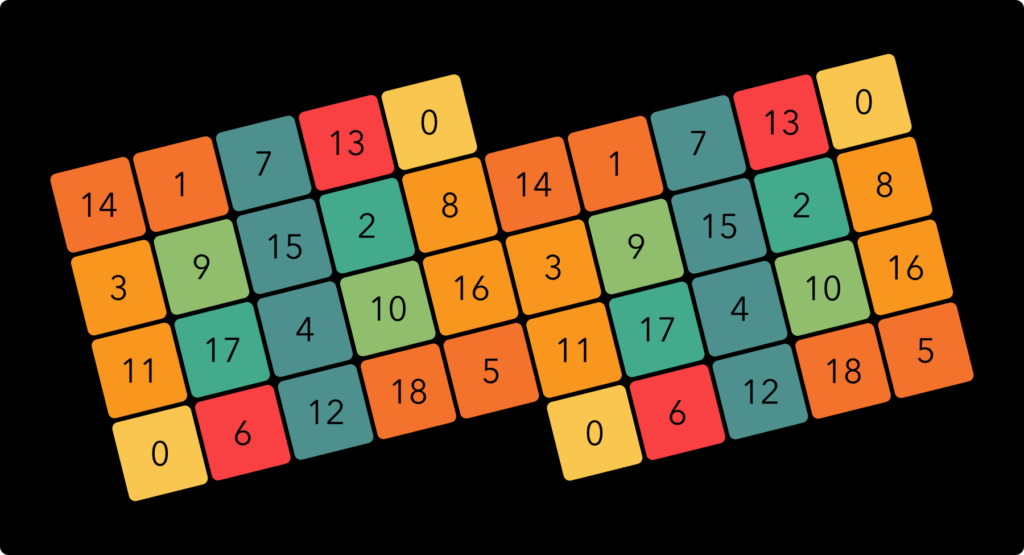
Because there are 19 different notes, a full octave uses 20 (just like a full octave in 12 EDO uses 13 notes). This means that the notes of 19 EDO can be conveniently arranged in a 4 by 5 grid. I’ve “glued” two of these grids together to expand the range, in such a way that horizontally, the notes ascend by 6 steps, which form a musical third, and vertically, they ascend by 11 steps, which form a musical fifth. This works out very well because five jumps of a fifth add up to one jump of a third (after octave reduction).
All the familiar notes of 12 EDO are present in 19 EDO, albeit in slightly altered versions, and besides that it offers 7 fresh new tonal colours.
The approximate ratios used for the colour scheme are as follows:
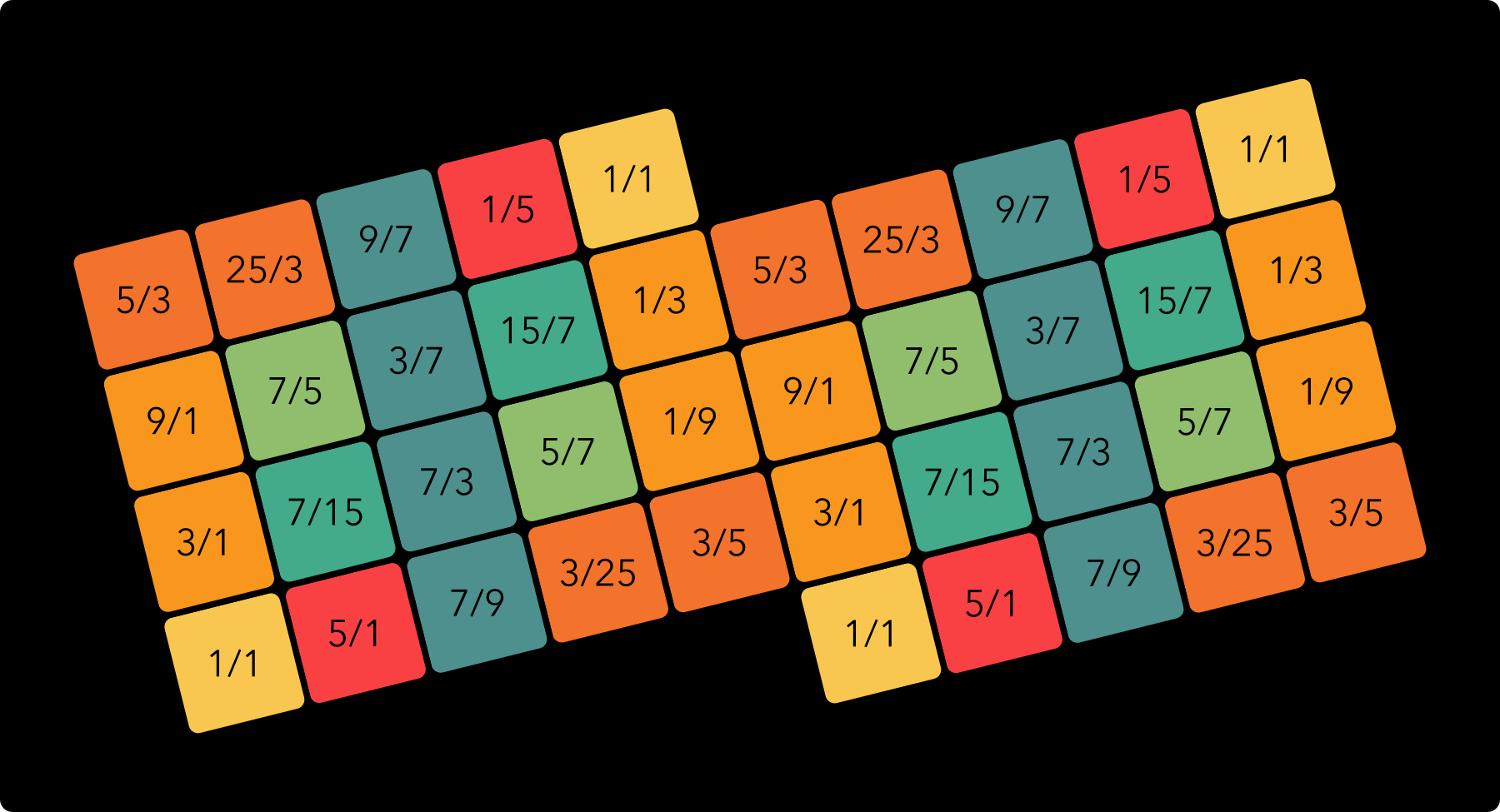
With note names instead of ratios, taking a D as the center, the map looks like this:
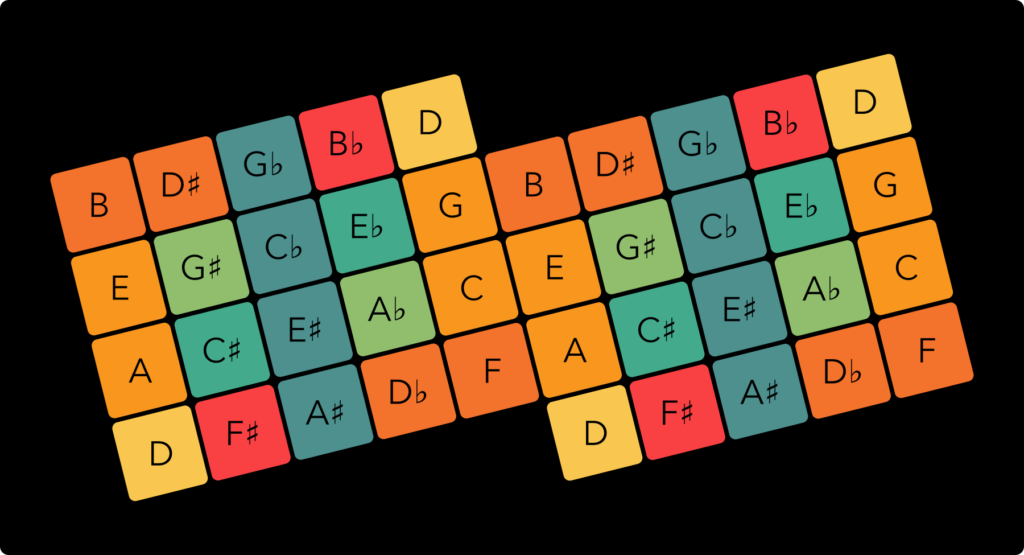
22 note Equal Temperament: the ‘EDO 22’ keyboard
This is the smallest temperament that provides reasonably good approximations of all the overtones up to the 11th harmonic (with ‘reasonably good’ roughly defined as ‘no more out of tune than the musical thirds in 12 EDO). It has a kind of rough and bluesy quality to it that I like very much. On the ‘EDO 22’ keyboard, the notes are arranged like this:
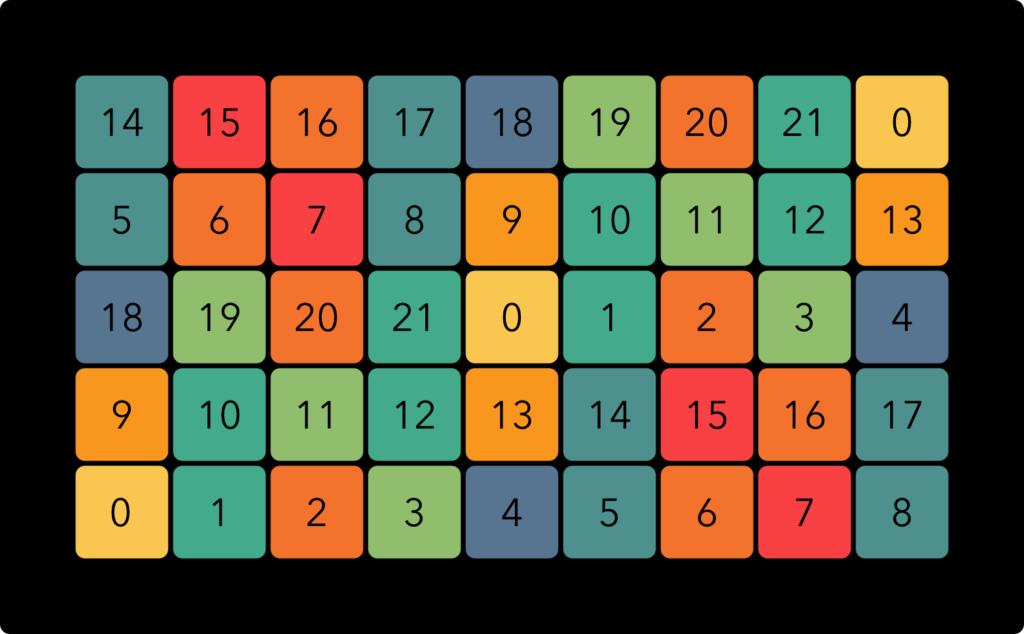
Horizontally, the notes are in ascending order from left to right. Vertically, each row up is a jump of 9 steps, which form a musical fourth. This layout is similar to the way the string are tuned on a guitar or bass, except in this case you have 5 horizontal “strings”.
The approximate ratios used for the colour scheme are as follows:
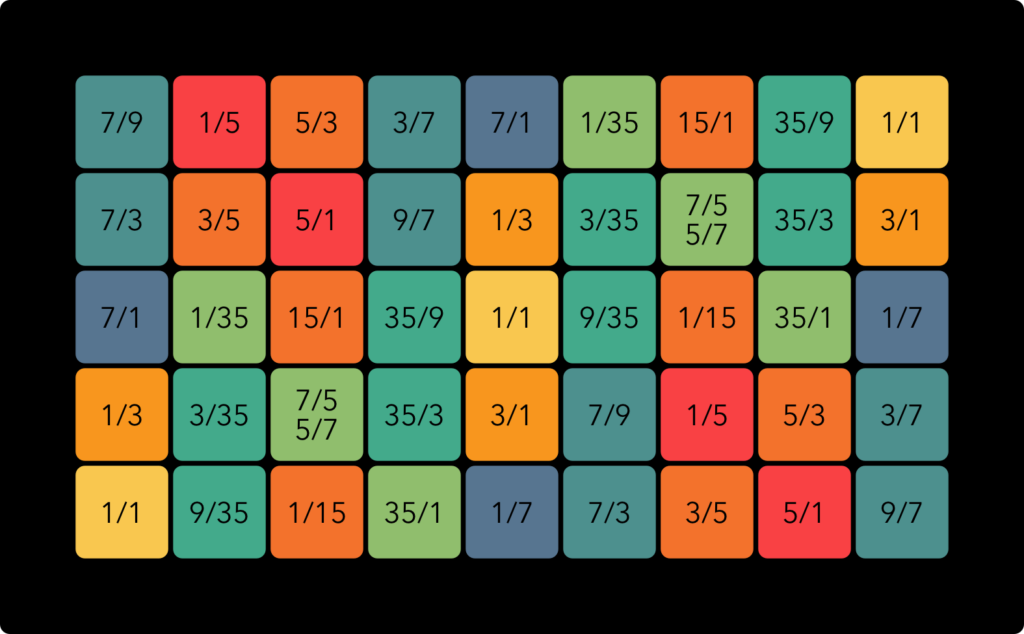
With note names instead of ratios, taking a D as the center, the map looks like this:
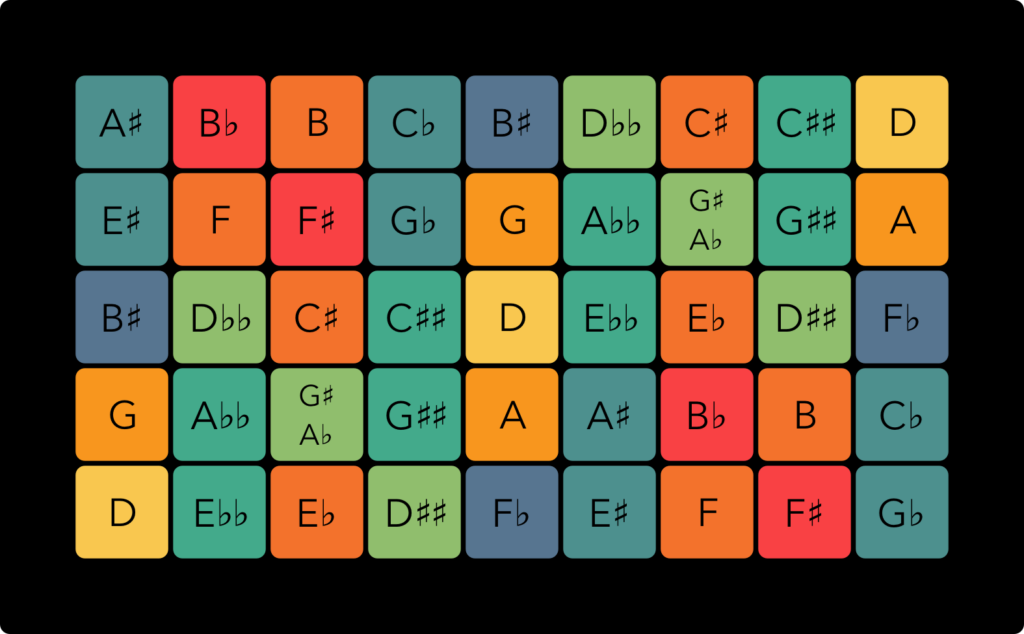
31 tone Equal Temperament: the ‘EDO 31’ keyboard
This temperament provides excellent approximations of all the overtones up to the 7th harmonic, and pretty good ones of the 11th and 13th harmonic as well. It is extremely close to quarter-comma meantone temperament, which was commonly used in European music before 12 EDO became the standard practice. It produces wonderfully clear harmonies and could have easily won out over 12 EDO if not for the much larger number of different notes. On the ‘EDO 31’ keyboard, the notes are arranged like this:
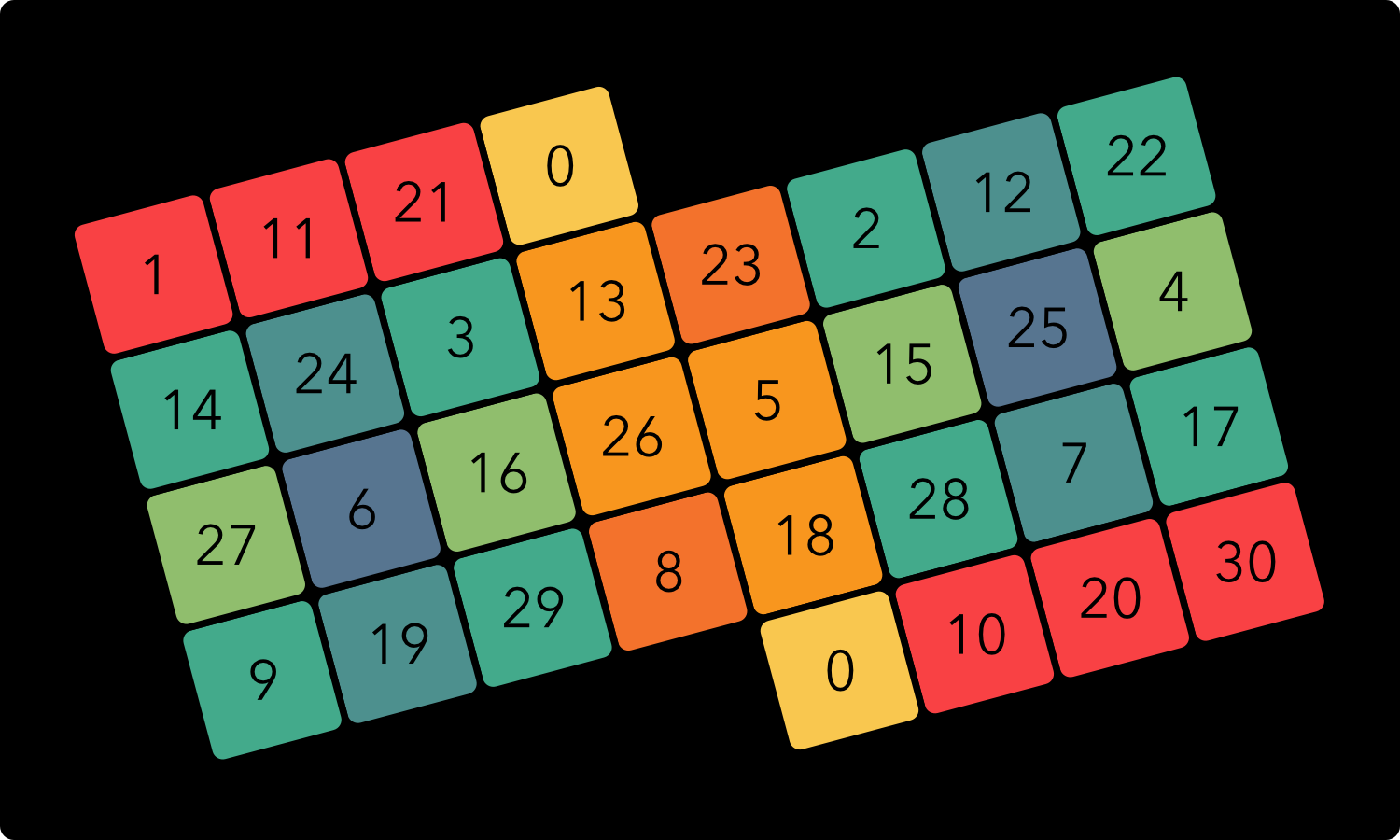
Horizontally, the notes ascend by 10 steps, which form a musical third. Vertically, the notes ascend by 18 steps, which form a musical fifth.
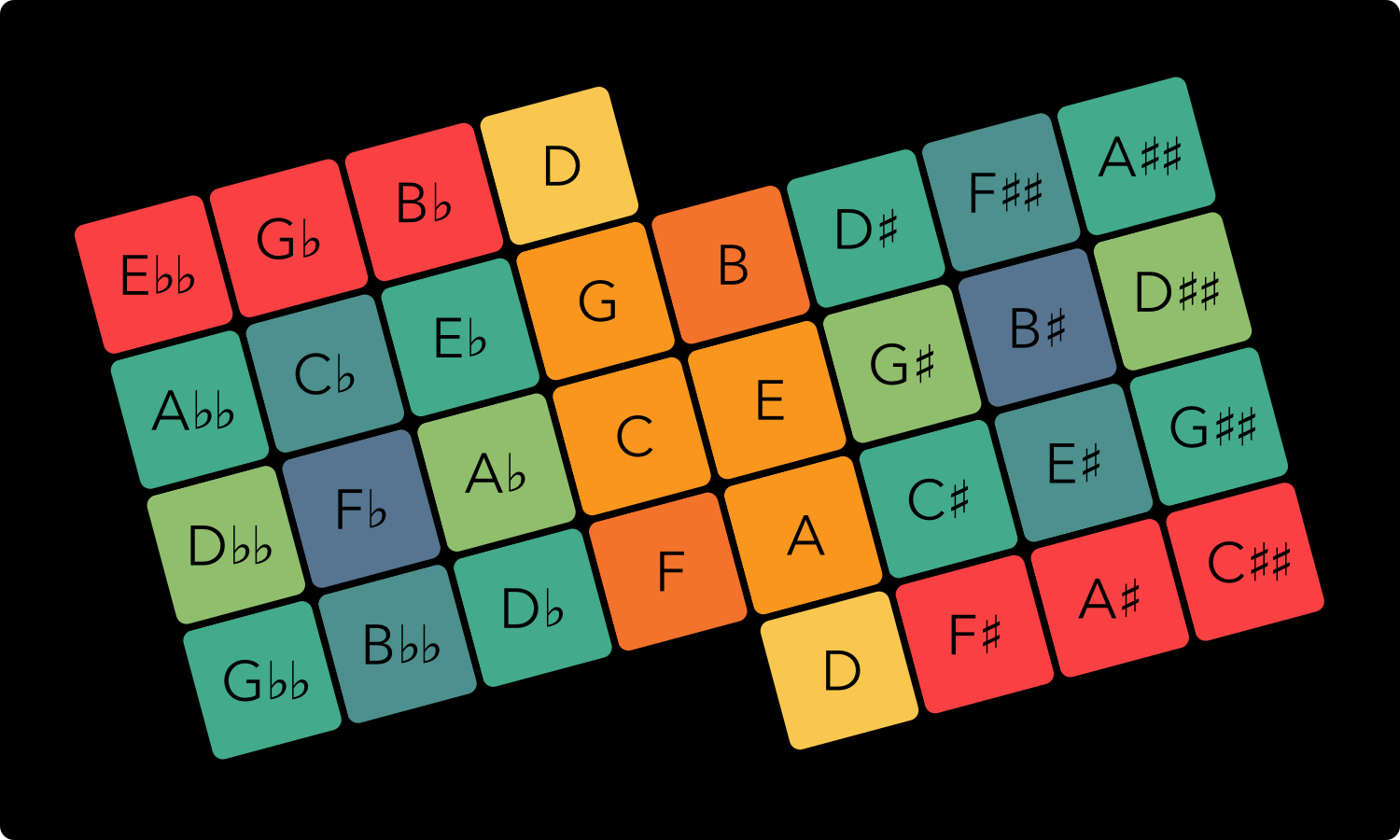
The approximate ratios used for the colour scheme are as follows:

With note names instead of ratios, taking a D as the center, the map looks like this:
53 tone Equal Temperament: the ‘EDO 53’ keyboard
This temperament is excellent for 5-limit intervals, with nearly perfectly tuned thirds and fifths. It also provides very decent approximations for higher harmonics all the way up to the 27th. It really has only one downside: 53 notes is a lot, making everything from constructing instruments to learning to play them quite complicated. On the ‘EDO 53’ keyboard, the notes are arranged like this:

Horizontally, the notes ascend by 31 steps, which form a musical fifth. Diagonally, the notes ascend by 17 steps, which form a musical third.
The approximate ratios used for the colour scheme are as follows:

With note names instead of ratios, taking a D as the center, the map looks like this:
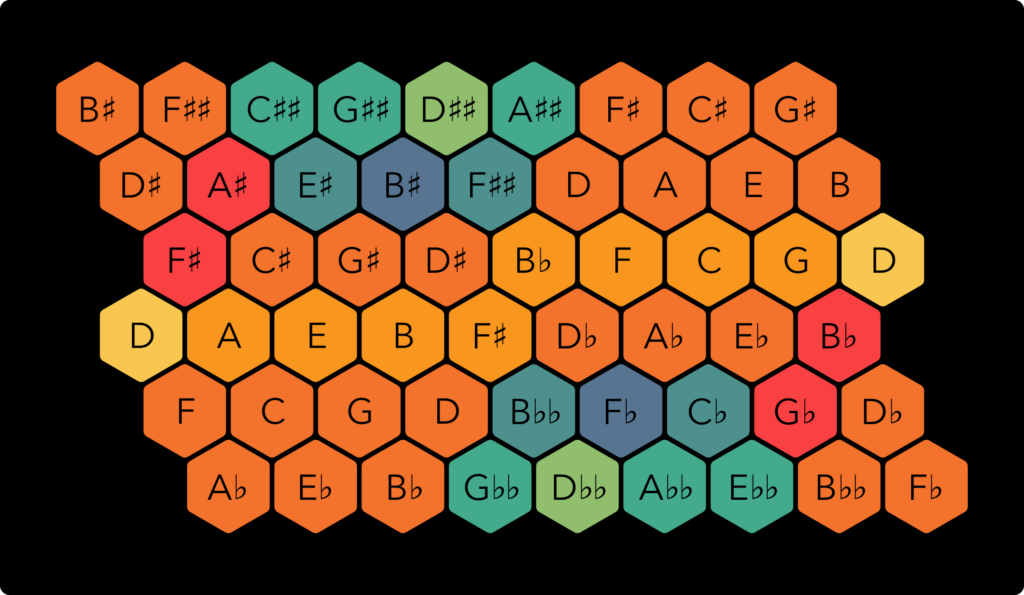
Reference chart of EDO notes, ratios and colours
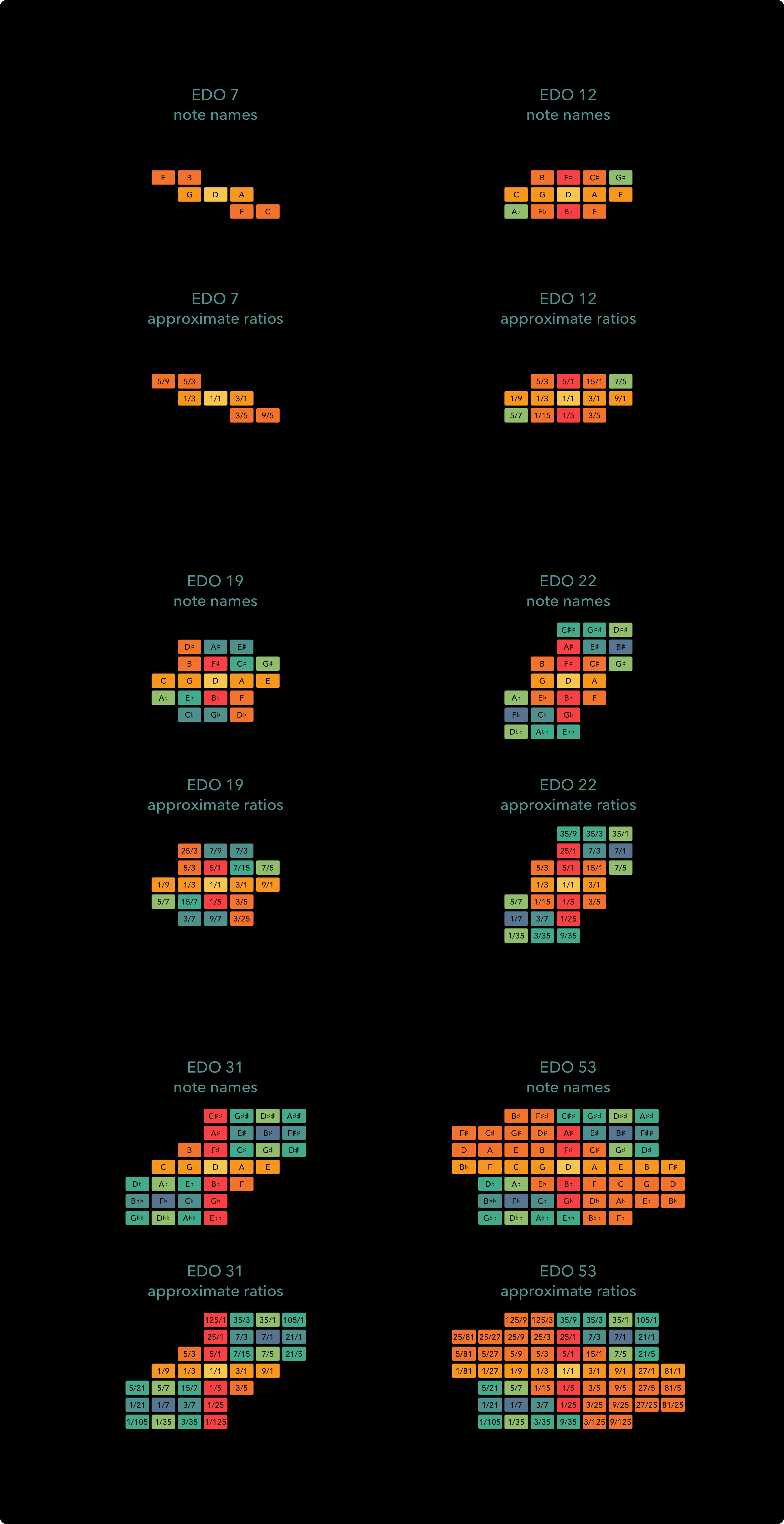
The chart above shows the notes of each EDO tuning system and the approximate ratios I have used for the colour scheme of the Arithmophone keyboards.
I hope this article explains some of the workings of the different Arithmophone keyboard styles and that it will encourage you to play around with them and experiment freely. If you have any feedback, corrections or suggestions, please let me know!
This page is part of my Arithmophone project.
Concept, design and development by Chiel Zwinkels © 2024
